假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下表格所示统计数据,由资料显示y对x呈线性相关关系。
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(Ⅰ)请根据上表的数据画出散点图并用最小二乘法求出y关于x的线性回归方程?
(Ⅱ)试根据(1)求出的线性回归方程,预测使用年限为10年时,维修费用是多少?
将圆
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线
.
(1)写出
的参数方程;
(2)设直线
与
的交点为
,以坐标原点为极点,
轴正半轴为极坐标建立极坐标系,求过线段
的中点且与
垂直的直线的极坐标方程.
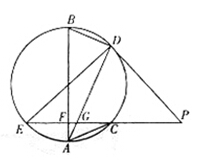
如图,
交圆于
、
两点,
切圆于
为
上一点且
,连接
并延长交圆于点
,作弦
垂直
,垂足为
.
(1)求证:
为圆的直径;
(2)若
,求证:
.
已知函数 , .证明:
(1)存在唯一
,使
;
(2)存在唯一
,使
,且对(1)中的
.
圆
的切线与
轴正半轴,
轴正半轴围成一个三角形,当该三角形面积最小时,切点为
(如图),双曲线
过点
且离心率为
.
(1)求
的方程;
(2)椭圆
过点P且与
有相同的焦点,直线
过
的右焦点且与
交于
两点,若以线段
为直径的圆心过点
,求
的方程.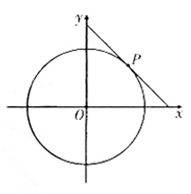
如图,
和
所在平面互相垂直,且
,
,
分别为
的中点.
(1)求证:
;
(2)求二面角
的正弦值.