已知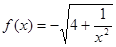 ,点
,点
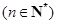 在函数
在函数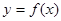 的图象上,
的图象上, .
.
(1)求数列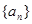 的通项公式;
的通项公式;
(2)数列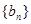 的前
的前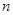 项和为
项和为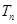 ,且满足
,且满足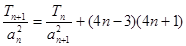 ,求证:
,求证: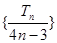 为等差数列;
为等差数列;
(3)求 的值,使得数列
的值,使得数列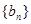 是等差数列,并求出
是等差数列,并求出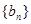 的通项公式.
的通项公式.
已知等差数列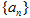 的前
的前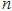 项和为
项和为 ,并且
,并且 ,
,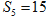 ,数列
,数列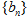 满足:
满足: ,
, ,记数列
,记数列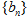 的前
的前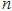 项和为
项和为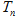 .
.
(Ⅰ)求数列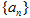 的通项公式
的通项公式 及前
及前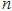 项和公式
项和公式 ;
;
(Ⅱ)求数列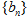 的通项公式
的通项公式 及前
及前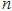 项和公式
项和公式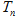 ;
;
(Ⅲ)记集合 ,若
,若 的子集个数为16,求实数
的子集个数为16,求实数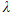 的取值范围。
的取值范围。
已知椭圆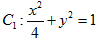 ,椭圆
,椭圆 以
以 的长轴为短轴,且与
的长轴为短轴,且与 有相同的离心率.
有相同的离心率.
(1)求椭圆 的方程;
的方程;
(2)设O为坐标原点,点A,B分别在椭圆 和
和 上,
上, 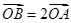 ,求直线
,求直线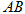 的方程.
的方程.
在△ABC中,角A,B,C所对的边分别为a,b,c,已知 .
.
(1)求角B的大小;
(2)若 ,求b的取值范围.
,求b的取值范围.
已知 是等比数列
是等比数列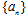 的前
的前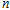 项和,
项和,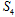 ,
, ,
,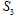 成等差数列,且
成等差数列,且 .
.
(Ⅰ)求数列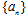 的通项公式;
的通项公式;
(Ⅱ)是否存在正整数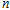 ,使得
,使得 ?若存在,求出符合条件的所有
?若存在,求出符合条件的所有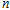 的集合;若不存在,说明理由.
的集合;若不存在,说明理由.
某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,顶部每平方米造价20元,求:
(1)仓库顶部面积 的最大允许值是多少?
的最大允许值是多少?
(2)为使 达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?