在某次考试中共有12道选择题,每道选择题有4个选项,其中只有一个是正确的,评分标准规定:“每题只选一项,答对得5分,不答或答错得0分”。某考生每道题给出一个答案,并已确定有9道题的答案是正确的,而其余题中,有一道题可判断出两个选项是错误的,有一道题可以判断出一个选项是错误的,还有一道题因不了解题意只能乱猜,试求出该考生;
(1)选择题得60分的概率;
(2)选择题所得分数 的数学期望。
的数学期望。
小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.
(1)根据图中的数据信息,写出众数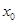 ;
;
(2)小明的父亲上班离家的时间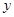 在上午
在上午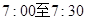 之间,而送报人每天在
之间,而送报人每天在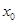 时刻前后
时刻前后
半小时内把报纸送达(每个时间点送达的可能性相等).
①求小明的父亲在上班离家前能收到报纸(称为事件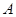 )的概率;
)的概率;
②求小明的父亲周一至周五在上班离家前能收到报纸的天数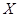 的数学期望.
的数学期望.
如图,在四棱锥 中,
中, 平面
平面 ,底面
,底面 是直角梯形,
是直角梯形, ,
,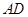 ∥
∥ ,且
,且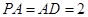 ,
,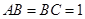 ,
,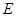 为
为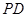 的中点.
的中点.
(1)设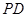 与平面
与平面 所成的角为
所成的角为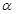 ,二面角
,二面角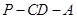 的大小为
的大小为 ,求证:
,求证: ;
;
(2)在线段 上是否存在一点
上是否存在一点 (与
(与 两点不重合),使得
两点不重合),使得 ∥平面
∥平面 ? 若存在,求
? 若存在,求 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
已知数列 是等差数列,
是等差数列, 是等比数列,其中
是等比数列,其中 ,
,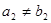 ,且
,且 为
为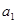 、
、 的等差中项,
的等差中项, 为
为 、
、 的等差中项.
的等差中项.
(1)求数列 与
与 的通项公式;
的通项公式;
(2)记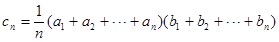 ,求数列
,求数列 的前
的前 项和
项和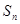 .
.
已知向量 ,设函数
,设函数
(1)求函数 的单调递增区间;
的单调递增区间;
(2)在 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且满足
,且满足 ,
, ,求
,求 的值.
的值.
设函数 .
.
(1)求 的最小正周期。
的最小正周期。
(2)若函数 与
与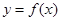 的图像关于直线
的图像关于直线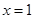 对称,求当
对称,求当 时
时 的最大值.
的最大值.