已知函数
 在一个周期内的图象如下图所示。
在一个周期内的图象如下图所示。
(1)求函数的解析式;
(2)设 ,且方程
,且方程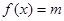 有两个不同的实数根,求实数m的取值范围和这两个根的和。
有两个不同的实数根,求实数m的取值范围和这两个根的和。
数列 满足
满足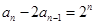
 ,且
,且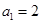 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 若 ,设数列
,设数列 的前
的前 项和为
项和为 ,求证:
,求证: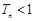 .
.
设函数 ,
, .
.
(1) 解不等式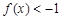 ;
;
(2) 设函数 ,且
,且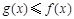 在
在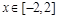 上恒成立,求实数
上恒成立,求实数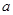 的取值范围.
的取值范围.
在极坐标系内,已知曲线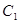 的方程为
的方程为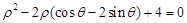 ,以极点为原点,极轴方向为
,以极点为原点,极轴方向为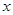 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线
正半轴方向,利用相同单位长度建立平面直角坐标系,曲线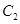 的参数方程为
的参数方程为 (
(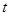 为参数).
为参数).
(1) 求曲线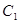 的直角坐标方程以及曲线
的直角坐标方程以及曲线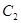 的普通方程;
的普通方程;
(2) 设点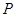 为曲线
为曲线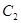 上的动点,过点
上的动点,过点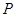 作曲线
作曲线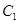 的两条切线,求这两条切线所成角余弦值的取值范围.
的两条切线,求这两条切线所成角余弦值的取值范围.
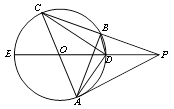
如图,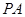 是
是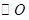 的切线,
的切线,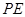 过圆心
过圆心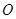 ,
, 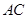 为
为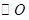 的直径,
的直径,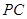 与
与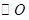 相交于
相交于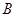 、
、 两点,连结
两点,连结 、
、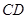 . (1) 求证:
. (1) 求证: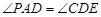 ;
;
(2) 求证: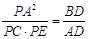 .
.
已知函数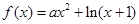 .
.
(1) 当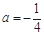 时,求函数
时,求函数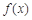 的单调区间;
的单调区间;
(2) 当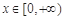 时,函数
时,函数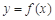 图象上的点都在
图象上的点都在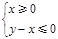 所表示的平面区域内,求实数
所表示的平面区域内,求实数 的取值范围.
的取值范围.
(3) 求证: ,(其中
,(其中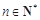 ,
, 是自然对数的底).
是自然对数的底).