如图，一个被等分成了3个相同扇形的圆形转盘，3个扇形分别标有数字1、3、6，指针的位置固定，转动转盘后任其自由停止，其中的某个扇形会恰好停止在指针所指的位置（指针指向两个扇形的交线时，重新转动转盘）.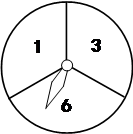
（1）请用画树状图或列表的方法(只选其中一种)，表示出分别转动转盘两次转盘自由停止后，指针所指扇形数字的所有结果；
（2）求分别转动转盘两次转盘自由停止后，指针所指扇形的数字之和的算术平方根为无理数的概率.
三角形纸片ABC（AB＞AC）沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展平纸片，如图；再次折叠该三角形纸片，使得点A与点D重合，折痕为EF，再次展平后连接DE、DF，如图，证明：四边形AEDF是菱形．
如图，在Rt△ABC中
，D、F分别是AB、AC的中点，延长BC到点E，使
求证：四边形DEBF是等腰梯形
如图，请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形
是平行四边形，并予以证明．（写出一种即可）关系：①
∥
，②
，③
，④
．
]
已知：在四边形
中， ， ；
求证：四边形是平行四边形．
某中学开展“五比五创”演讲比赛活动，九(1)班准备根据根据平时练习成绩准备从张华、李明2名选手选出一名参加比赛，他们两人的五次平时成绩（满分20分）如下图所示。
（1）根据下图，分别求出张华、李明的平均成绩和方差；
（2）根据（1）的计算结果，分析张华、李明同学各自的优点，并决定让那位同学参加比赛？
阅读下列解题过程：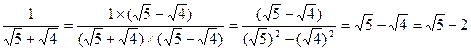 
；
。
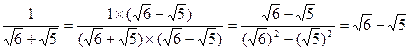请回答下列问题：
（1）观察上面的解题过程，请直接写出式子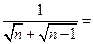
；
（2）利用上面所提供的解法，请化简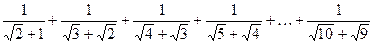
的值。