已知数列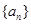 中,
中,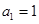 ,
,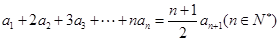
(Ⅰ)求数列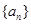 的通项公式;
的通项公式;
(Ⅱ)求数列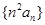 的前
的前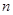 项和
项和 ;
;
(Ⅲ)(理科)若存在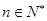 ,使得
,使得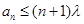 成立,求实数
成立,求实数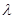 的最小值。
的最小值。
已知关于x的不等式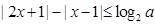 (其中
(其中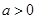 )。
)。
(1)当a=4时,求不等式的解集;
(2)若不等式有解,求实数a的取值范围。
在极坐标系中,曲线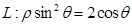 ,过点A(5,α)(α为锐角且
,过点A(5,α)(α为锐角且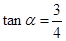 )作平行于
)作平行于 的直线
的直线 ,且
,且 与曲线L分别交于B,C两点。
与曲线L分别交于B,C两点。
(1)以极点为原点,极轴为x轴的正半轴,取与极坐标相同单位长度,建立平面直角坐标系,写出曲线L和直线 的普通方程;
的普通方程;
(2)求|BC|的长。
如图,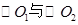 相交于A、B两点,AB是
相交于A、B两点,AB是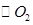 的直径,过A点作
的直径,过A点作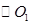 的切线交
的切线交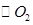 于点E,并与BO1的延长线交于点P,PB分别与
于点E,并与BO1的延长线交于点P,PB分别与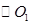 、
、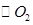 交于C,D两点。
交于C,D两点。
求证:(1)PA·PD=PE·PC;
(2)AD=AE。
如图,F1,F2是离心率为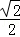 的椭圆C:
的椭圆C: (a>b>0)的左、右焦点,直线l:x=﹣
(a>b>0)的左、右焦点,直线l:x=﹣ 将线段F1F2分成两段,其长度之比为1:3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1:3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
(1)求椭圆C的方程;
(2)求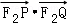 的取值范围.
的取值范围.
已知数列{an}中,a1=1,an>0,an+1是函数f(x)= x3+
x3+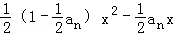 的极小值点.
的极小值点.
(1)证明数列{an}为等比数列,并求出通项公式an;
(2)设bn=nan2,数列{bn}的前n项和为Sn,求证: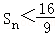 .
.