山东省某示范性高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座。(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座概率如下表:
| |
信息技术 |
生物 |
化学 |
物理 |
数学 |
| 周一 |
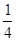 |
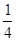 |
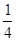 |
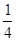 |
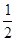 |
| 周三 |
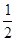 |
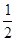 |
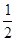 |
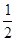 |
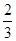 |
| 周五 |
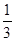 |
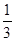 |
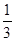 |
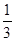 |
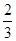 |
(Ⅰ)求数学辅导讲座在周一、周三、周五都不满座的概率;
(Ⅱ)设周三各辅导讲座满座的科目数为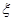 ,求随即变量
,求随即变量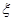 的分布列和数学期望
的分布列和数学期望
当12点过15分的时候,时钟长短针的夹角是多少度?
(10分)一根长为l的线,一端固定,另一端悬挂一个小球,如图.已知小球从M点放下,经过0.5秒第一次到达平衡位置O.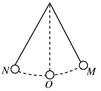
(1)求小球第三次经过平衡位置O的时间.
(2)求小球运动的周期.
(3)经过7.2秒,小球是在平衡位置的右边还是左边?
在与角-2 010°终边相同的角中,求满足下列条件的角.
(1)最小的正角;
(2)最大的负角;
(3)-720°~720°内的角.
已知角α的终边与-120°角的终边关于y轴对称.求α.
(本题10分)已知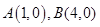 ,动点
,动点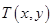 满足
满足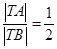 ,设动点
,设动点 的轨迹是曲线
的轨迹是曲线 ,直线
,直线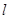 :
: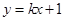 与曲线
与曲线 交于
交于 两点.(1)求曲线
两点.(1)求曲线 的方程;
的方程;
(2)若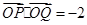 ,求实数
,求实数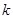 的值;
的值;
(3)过点 作直线
作直线 与
与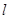 垂直,且直线
垂直,且直线 与曲线
与曲线 交于
交于 两点,求四边形
两点,求四边形 面积的最大值.
面积的最大值.