在四棱锥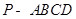 中,
中,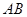 //
//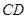 ,
,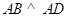 ,
,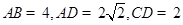 ,
,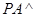 平面
平面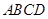 ,
,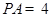 .
.
(Ⅰ)设平面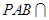 平面
平面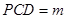 ,求证:
,求证: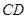 //
// ;
;
(Ⅱ)求证: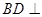 平面
平面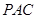 ;
;
(Ⅲ)设点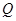 为线段
为线段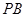 上一点,且直线
上一点,且直线 与平面
与平面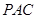 所成角的正弦值为
所成角的正弦值为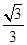 ,求
,求 的值.
的值.
如图,四棱锥 P﹣ ABCD中,侧面 PAD为等边三角形且垂直于底面 ABCD, AB= BC AD,∠ BAD=∠ ABC=90°.
(1)证明:直线 BC∥平面 PAD;
(2)若△ PCD面积为2 ,求四棱锥 P﹣ ABCD的体积.

已知等差数列{ a n}的前 n项和为 S n,等比数列{ b n}的前 n项和为 T n, a 1=﹣1, b 1=1, a 2+ b 2=2.
(1)若 a 3+ b 3=5,求{ b n}的通项公式;
(2)若 T 3=21,求 S 3.
[选修4-5:不等式选讲]
已知函数 .
(1)当 时,求不等式 的解集;
(2)若不等式 的解集包含 ,求 a的取值范围.
[选修4―4:坐标系与参数方程]
在直角坐标系 中,曲线 C的参数方程为 ,直线 l的参数方程为 .
(1)若 ,求 C与 l的交点坐标;
(2)若 C上的点到 l的距离的最大值为 ,求a.
已知函数 .
(1)讨论 的单调性;
(2)若 有两个零点,求a的取值范围.