在长方体ABCD-A1B1C1D1中,AB=2,BC=B1B=1,M、N分别是AD、DC的中点.
(1)求证:MN//A1C1;
(2)求:异面直线MN与BC1所成角的余弦值.
已知数列{an}中,a1= 1,前 项和为
项和为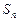 ,且
,且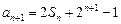 (n∈N*)
(n∈N*)
(1)求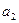 与
与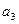 的值;
的值;
(2)设 ,
,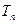 是数列
是数列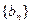 的前
的前 项和,求数列
项和,求数列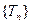 的通项公式.
的通项公式.
已知直角梯形ABCD中, ,
,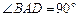 ,且
,且 ,点E、F分别在AD、BC上,满足
,点E、F分别在AD、BC上,满足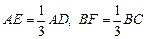 .现将此梯形沿EF折叠成如图所示图形,且使
.现将此梯形沿EF折叠成如图所示图形,且使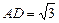 .
.
(1)求证:AE⊥平面ABCD;
(2)求二面角 的大小.
的大小.
“星光大道”是观众喜爱的央视栏目.现有3位周冠军A、B、C和甲、乙两位挑战者参加月冠军比赛,比赛规则是:第一轮甲、乙两位挑战者从3位周冠军中各选一位进行比赛,胜者进入第二轮比赛,未被选中的周冠军直接进入第二轮比赛;第二轮比赛从3位选手中淘汰一位,胜者进入第三轮比赛;第三轮比赛胜者为月冠军.每位选手被淘汰的可能性相同.
(1)求周冠军A、B和挑战者甲、乙进行第一轮比赛,且至少有一位挑战者进入第二轮比赛的概率;
(2)求月冠军是挑战者的概率;
已知△ABC中,角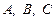 所对边长分别是
所对边长分别是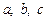 ,设函数
,设函数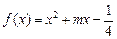 为偶函数,且
为偶函数,且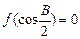 .
.
(1)求角B的大小;
(2)若△ABC的面积为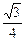 ,其外接圆的半径为
,其外接圆的半径为 ,求△ABC的周长.
,求△ABC的周长.
(本小题满分12分)已知函数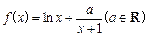 .
.
(I)当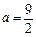 时,如果关于
时,如果关于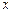 的方程:
的方程: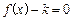 有且只有一个解,求实数
有且只有一个解,求实数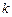 的取值范围;
的取值范围;
(II)当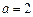 时,试比较
时,试比较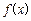 与1的大小;
与1的大小;
(Ⅲ)求证: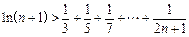
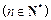 .
.