设函数 ,
,
(1)当 时,求函数
时,求函数 的单调递减区间;
的单调递减区间;
(2)若函数 有相同的极大值,且函数
有相同的极大值,且函数 在区间
在区间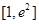 上的
上的
最大值为 ,求实数
,求实数 的值.(其中e是自然对数的底数).
的值.(其中e是自然对数的底数).
已知函数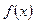 的定义域为R,且满足以下条件:1对任意的
的定义域为R,且满足以下条件:1对任意的 ,有
,有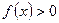 ;2对任意
;2对任意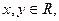 有
有 ;3
;3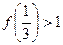
(Ⅰ)求 的值;
的值;
(Ⅱ)判断 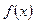 的单调性,并说明理由;
的单调性,并说明理由;
(Ⅲ)若 且a,b,c成等比数列,求证:
且a,b,c成等比数列,求证: .
.
已知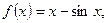 数列
数列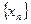 满足
满足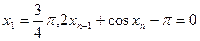
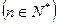
(Ⅰ) 判断并证明函数f(x)的单调性;
(Ⅱ) 设数列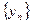 满足
满足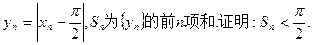
已知函数 为偶函数,且其图象上相邻两个最大值点之间的距离为
为偶函数,且其图象上相邻两个最大值点之间的距离为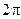 。
。
(1)求函数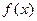 的表达式。(2)若
的表达式。(2)若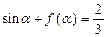 ,求
,求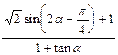 的值。
的值。
某抛物线形拱桥跨度是20米,拱高4米,在建桥时每隔4米需用一支柱支撑,求其中最长的支柱的长.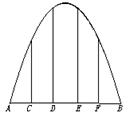
已知椭圆的中心在坐标原点,焦点在x轴上,它的一个焦点为F,M是椭圆上的任意点,|MF|的最大值和最小值的几何平均数为2,椭圆上存在着以y=x为轴的对称点M1和M2,且|M1M2|=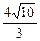 ,试求椭圆的方程
,试求椭圆的方程