(本小题满分12分)四棱锥A-BCDE的正视图和俯视图如下,其中正视图是等边三角形,俯视图是直角梯形.
(I)若F为AC的中点,当点M在棱AD上移动时,是否总有BF丄CM,请说明理由.
(II)求三棱锥C_ADE的高.
(本小题满分12分)甲、乙两所学校的代表队参加汉字听写大赛.在比赛第二阶段,两队各剩最后两名队员上场.甲队两名队员通过第二阶段比赛的概率分别是 和
和 ,乙队两名队员通过第二阶段比赛的概率都是
,乙队两名队员通过第二阶段比赛的概率都是 .通过了第二阶段比赛的队员,才能进入第三阶段比赛(若某队两个队员都没有通过第二阶段的比赛,则该队进入第三阶段比赛人数为
.通过了第二阶段比赛的队员,才能进入第三阶段比赛(若某队两个队员都没有通过第二阶段的比赛,则该队进入第三阶段比赛人数为 ).所有参赛队员比赛互不影响,其过程、结果都是彼此独立的.
).所有参赛队员比赛互不影响,其过程、结果都是彼此独立的.
(Ⅰ)求第三阶段比赛,甲、乙两队人数相等的概率;
(Ⅱ) 表示第三阶段比赛甲、乙两队的人数差的绝对值,求
表示第三阶段比赛甲、乙两队的人数差的绝对值,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)某军区新兵 步枪射击个人平均成绩
步枪射击个人平均成绩 (单位:环)服从正态分布
(单位:环)服从正态分布 ,从这些个人平均成绩中随机抽取
,从这些个人平均成绩中随机抽取 个,得到如下频数分布表:
个,得到如下频数分布表:
 |
 |
 |
 |
 |
 |
 |
| 频数 |
 |
 |
 |
 |
 |
 |
(Ⅰ)求 和
和 的值(用样本数学期望、方差代替总体数学期望、方差);
的值(用样本数学期望、方差代替总体数学期望、方差);
(Ⅱ)如果这个军区有新兵 名,试估计这个军区新兵
名,试估计这个军区新兵 步枪射击个人平均成绩在区间
步枪射击个人平均成绩在区间 上的人数
上的人数
[参考数据: ,若
,若 ,则
,则 ,
, ,
, ].
].
(本小题满分12分)下表是随机抽取的某市五个地段五种不同户型新电梯房面积 (单位:十平方米)和相应的房价
(单位:十平方米)和相应的房价 (单位:万元)统计表:
(单位:万元)统计表:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(Ⅰ)在给定的坐标系中画出散点图;
(Ⅱ)求用最小二乘法得到的回归直线方程(参考公式和数据: ,
, ,
, );
);
(Ⅲ)请估计该市一面积为
 的新电梯房的房价.
的新电梯房的房价.
(本题12分)已知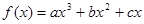 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间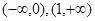 上是减函数,又
上是减函数,又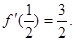
(Ⅰ)求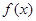 的解析式;
的解析式;
(Ⅱ)若在区间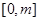 (m>0)上恒有
(m>0)上恒有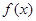 ≤x成立,求m的取值范围.
≤x成立,求m的取值范围.
(本小题满分12分)已知方程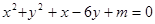
(1)若此方程表示的曲线是圆C,求m的取值范围;
(2)若(1)中的圆C与直线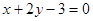 相交于P,Q两点,且
相交于P,Q两点,且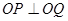 (O为原点),求圆C的方程.
(O为原点),求圆C的方程.