(本小题满分12分)设平面向量 ="(m,1),"
="(m,1),"  =(2,n),其中m,n∈{1,2,3,4}.
=(2,n),其中m,n∈{1,2,3,4}.
(Ⅰ)请列出有序数组(m,n)的所有可能结果;
(Ⅱ)若“使得 ⊥(
⊥( -
- )成立的(m,n)”为事件A,求事件A发生的概率。
)成立的(m,n)”为事件A,求事件A发生的概率。
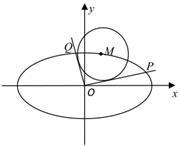
如图,已知 是椭圆
是椭圆 :
: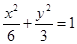 上的任一点,从原点
上的任一点,从原点 向圆
向圆 :
: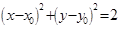 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 、
、 .
.
(1)若直线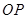 ,
,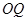 的斜率存在,并记为
的斜率存在,并记为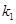 ,
,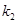 ,求证:
,求证: 为定值;
为定值;
(2)试问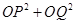 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
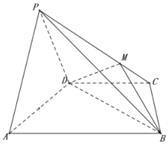
如图,在四棱锥 中,底面梯形
中,底面梯形 中,
中, ,平面
,平面 平面
平面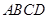 ,
,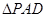 是等边三角形,已知
是等边三角形,已知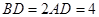 ,
, ,
, ,且
,且 .
.
(1)求证:平面 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)试确定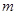 的值,使三棱锥
的值,使三棱锥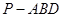 体积为三棱锥
体积为三棱锥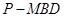 体积的3倍.
体积的3倍.
已知 的角
的角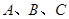 的对边分别为
的对边分别为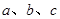 ,其面积
,其面积 ,
,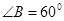 ,且
,且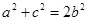 ;等差数列
;等差数列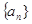 中,且
中,且 ,公差
,公差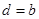 .数列
.数列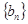 的前
的前 项和为
项和为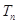 ,且
,且 ,
,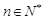 .
.
(1)求数列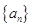 、
、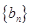 的通项公式;
的通项公式;
(2)设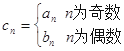 , 求数列
, 求数列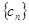 的前
的前 项和
项和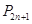 .
.
株洲市某中学利用周末组织教职员工进行了一次秋季登石峰山健身的活动,有 人参加,现将所有参加人员按年龄情况分为
人参加,现将所有参加人员按年龄情况分为 ,
, ,
, ,
, ,
, ,
, ,
,  等七组,其频率分布直方图如下图所示.已知
等七组,其频率分布直方图如下图所示.已知 之间的参加者有8人.
之间的参加者有8人.
(1)求 和
和 之间的参加者人数
之间的参加者人数 ;
;
(2)已知 和
和 之间各有
之间各有 名数学教师,现从这两个组中各选取
名数学教师,现从这两个组中各选取 人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有
人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有 名数学教师的概率?
名数学教师的概率?
(3)组织者从 之间的参加者(其中共有
之间的参加者(其中共有 名女教师,其余全为男教师)中随机选取
名女教师,其余全为男教师)中随机选取 名担任后勤保障工作,其中女教师的人数为
名担任后勤保障工作,其中女教师的人数为 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.
函数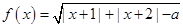 .
.
(1)若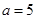 ,求函数
,求函数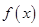 的定义域
的定义域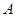 ;
;
(2)设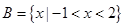 ,当实数
,当实数 时,证明:
时,证明: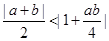 .
.