中国 黄石第三届国际矿冶文化旅游节将于2012年8月20日在黄石铁山举行,为了搞好接待工作,组委会准备在湖北理工学院和湖北师范学院分别招募8名和12名志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
黄石第三届国际矿冶文化旅游节将于2012年8月20日在黄石铁山举行,为了搞好接待工作,组委会准备在湖北理工学院和湖北师范学院分别招募8名和12名志愿者,将这20名志愿者的身高编成如下茎叶图(单位:cm)
若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有湖北师范学院的“高个子”才能担任“兼职导游”。
(1)根据志愿者的身高编茎叶图指出湖北师范学院志愿者身高的中位数;
(2)如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(3)若从所有“高个子”中选3名志愿者,用 表示所选志愿者中能担任“兼职导游”的人数,试写出
表示所选志愿者中能担任“兼职导游”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望。
的数学期望。
在对人们休闲的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)画出三维柱形图和二维条形图;
(3)检验性别是否与休闲方式有关,可靠性有多大。
已知数列 为其前n项和,计算得
为其前n项和,计算得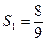 ,
, ,观察上述结果,推测出计算Sn的公式,并用数学归纳法加以证明。
,观察上述结果,推测出计算Sn的公式,并用数学归纳法加以证明。
已知ΔABC的三条边分别为 求证:
求证:
通过计算可得下列等式:


┅┅
将以上各式分别相加得:
即:
类比上述求法:请你求出 的值.
的值.
设函数 .
.
(1)证明: ;
;
(2)设 为
为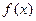 的一个极值点,证明
的一个极值点,证明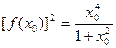 .
.