如图所示,四边形ABCD为矩形,点M是BC的中点,CN= CA,用向量法证明:
CA,用向量法证明:
(1)D、N、M三点共线;(2)若四边形ABCD为正方形,则DN=BN. 

如图,已知点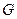 是边长为
是边长为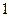 的正三角形
的正三角形 的中心,线段
的中心,线段 经过点
经过点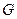 ,并绕点
,并绕点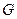 转动,分别交边
转动,分别交边 、
、 于点
于点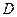 、
、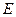 ;设
;设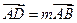 ,
,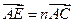 ,其中
,其中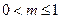 ,
, .
.
(1)求表达式 的值,并说明理由;
的值,并说明理由;
(2)求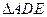 面积的最大和最小值,并指出相应的
面积的最大和最小值,并指出相应的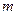 、
、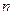 的值.
的值.
设全集 ,关于
,关于 的不等式
的不等式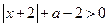 (
( )的解集为
)的解集为 .
.
(1)分别求出当 和
和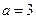 时的集合
时的集合 ;
;
(2)设集合 ,若
,若 中有且只有三个元素,求实数
中有且只有三个元素,求实数 的取值范围.
的取值范围.
如图, 是圆柱体
是圆柱体 的一条母线,
的一条母线, 过底面圆的圆心
过底面圆的圆心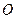 ,
, 是圆
是圆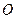 上不与点
上不与点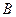 、
、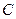 重合的任意一点,已知棱
重合的任意一点,已知棱 ,
,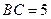 ,
,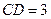 .
.
(1)求直线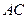 与平面
与平面 所成的角的大小;
所成的角的大小;
(2)将四面体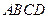 绕母线
绕母线 转动一周,求
转动一周,求 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.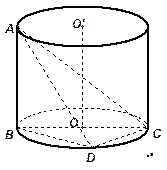
已知椭圆的一个焦点F1(0,-2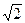 ),对应的准线方程为y=-
),对应的准线方程为y=- ,且离心率e满足:
,且离心率e满足: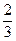 ,e,
,e,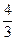 成等比数列.
成等比数列.
(1)求椭圆方程;
(2)是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰被直线x=-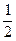
平分.若存在,求出l的倾斜角的范围;若不存在,请说明理由.
中华人民共和国个人所得税法》规定,公民月工资,薪金所得不超过1600元的部分不必纳税,超过1600元的部分为全月应纳税所得额,此项税款按下表分段累进计算:
| 全月应纳税所得额 |
税率 |
| 不超过500元的部分 |
5% |
| 超过500元的部分至2000元的部分 |
10% |
(1)试写出工资x (x 3600 元)与税收 y的函数关系式。
3600 元)与税收 y的函数关系式。
(2)给出计算应纳税所得额的伪代码。
(3)学校王老师今年9月税后工资为2390元,请问王老师9月纳税多少元?