已知平面向量 =(
=( ,1),
,1), =(
=(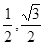 ),
),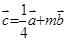 ,
, ,
, .
.
(1)当 时,求
时,求 的取值范围;
的取值范围;
(2)设 ,是否存在实数
,是否存在实数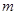 ,使得
,使得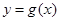 有最大值2,若存在,求出所有满足条件的
有最大值2,若存在,求出所有满足条件的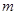 值,若不存在,说明理由
值,若不存在,说明理由
某超市在节日期间进行有奖促销,规定凡在该超市购物满400元的顾客,均可获得一次摸奖机会.摸奖规则如下:
奖盒中放有除颜色不同外其余完全相同的4个球(红、黄、黑、白).顾客不放回的每次摸出1个球,若摸到黑球则摸奖停止,否则就继续摸球.按规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次摸奖停止的概率;
(2)记 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量 的分布列和数学期望.
的分布列和数学期望.
已知 均为正数,证明:
均为正数,证明: .
.
在平面直角坐标系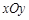 中,直线
中,直线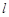 的参数方程是
的参数方程是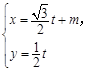 (t是参数), 以原点为极点,x轴的正半轴为极轴建立极坐标系,若圆C的极坐标方程是ρ=4cosθ,且直线
(t是参数), 以原点为极点,x轴的正半轴为极轴建立极坐标系,若圆C的极坐标方程是ρ=4cosθ,且直线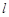 与圆C相切,求实数m的值.
与圆C相切,求实数m的值.
已知矩阵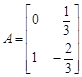 ,求点
,求点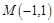 在矩阵
在矩阵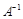 对应的变换作用下得到的点
对应的变换作用下得到的点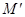 坐标.
坐标.
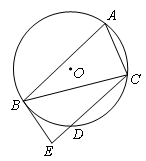
如图,A,B,C是⊙O上的三点,BE切⊙O于点B,D是 与⊙O的交点.若
与⊙O的交点.若 ,
,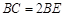 ,求证:
,求证: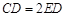 .
.