已知直线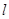 :
: (k
(k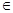 R)与圆C:
R)与圆C: 相交于点A、B, M为弦AB中点.
相交于点A、B, M为弦AB中点.
(Ⅰ) 当k=1时,求弦AB的中点M的坐标及AB弦长;
(Ⅱ)求证:直线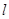 与圆C总有两个交点;
与圆C总有两个交点;
(Ⅲ)当k变化时求弦AB的中点M的轨迹方程.
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的200天内,西红柿的种植成本与上市时间的关系用图1的抛物线弧表示,西红柿市场售价与上市时间的关系用图2的一条线段表示(注:市场售价和种植成本的单位:元/100kg,时间单位:天)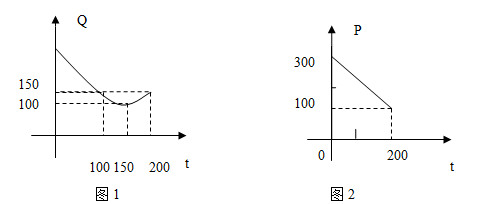
(1)写出图1表示的种植成本与时间的函数关系式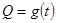 ,写出图2表示的市场售价与时间的函数关系式
,写出图2表示的市场售价与时间的函数关系式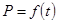
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
已知函数 是定义在
是定义在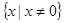 上的偶函数,且当
上的偶函数,且当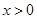 时,
时,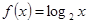 .
.
(1)求出函数 的解析式;
的解析式;
(2)画出函数 的图象,并根据图象写出函数
的图象,并根据图象写出函数 的增区间;
的增区间;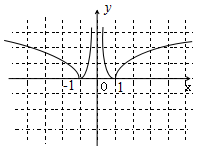
(3)设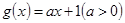 ,对任意
,对任意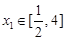 ,存在
,存在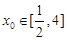 使
使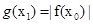 ,求
,求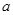 的取值范围.
的取值范围.
设集合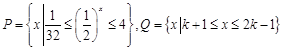
(1)化简集合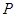 ,并求当
,并求当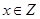 时,
时,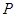 的真子集的个数.
的真子集的个数.
(2)若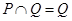 ,求实数
,求实数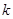 的取值范围.
的取值范围.
已知全集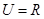 ,集合
,集合 ,
, .
.
(1)求 和
和 ;
;
(2)求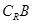 ;
;
(3)定义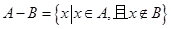 ,求
,求 ,
, .
.
求值:
(1) ;
;
(2) +
+ .
.