已知函数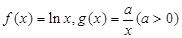 ,设
,设
(1)求 的单调区间;
的单调区间;
(2)若以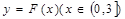 图象上任意一点
图象上任意一点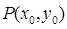 为切点的切线的斜率
为切点的切线的斜率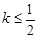 恒成立,求实数的最小值;
恒成立,求实数的最小值;
(3)是否存在实数 ,使得函数
,使得函数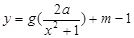 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
(本小题满分12分)
在数列 中,
中,
(1)设 求数列
求数列 的通项公式
的通项公式
(2)求数列 的前
的前 项和
项和 。
。
(本题12分)一缉私艇发现在方位角45°方向,距离12海里的海面上有一走私船正以10海里/小时的速度沿方位角为105°方向逃窜,若缉私艇的速度为14海里/小时,缉私艇沿方位角45°+α的方向追去,若要在最短的时间内追上该走私船,求追击所需时间和α角的正弦.(注:方位角是指正北方向按顺时针方向旋转形成的角,设缉私艇与走私船原来的位置分别为A、C,在B处两船相遇). 
(本题12分)设 是公比大于1的等比数列,已知
是公比大于1的等比数列,已知 ,且
,且 构成等差数列.
构成等差数列.
(1)求数列 的通项公式.(2)令
的通项公式.(2)令 求数列
求数列 的前
的前 项和
项和 .
.
(本小题满分12分)
已知 、
、 、
、 为
为 的三内角,且其对边分别为
的三内角,且其对边分别为 、
、 、
、 ,若
,若 .
.
(Ⅰ)求 ; (Ⅱ)若
; (Ⅱ)若 ,求
,求 的面积
的面积
(本小题满分10分)已知数列 的前
的前 项和
项和 ,
, 求 数列
求 数列 的通项公式及数列
的通项公式及数列 的前
的前 项和
项和 。
。