已知函数 (
(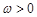 ,
, ),且函数
),且函数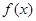 的最小正周期为
的最小正周期为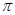 .
.
(1)求函数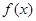 的解析式并求
的解析式并求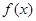 的最小值;
的最小值;
(2)在 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为 ,若
,若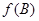 =1,
=1, ,且
,且 ,求边长
,求边长 .
.
如图,在直角坐标系中,已知△PAB的周长为8,且点A,B的坐标分别为(-1,0),(1,0).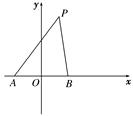
(1)试求顶点P的轨迹C1的方程;
(2)若动点C(x1,y1)在轨迹C1上,试求动点Q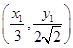 的轨迹C2的方程.
的轨迹C2的方程.
已知函数f(x)=ax+ln x,其中a为常数,e为自然对数的底数.
(1)当a=-1时,求f(x)的最大值;
(2)当a=-1时,试推断方程|f(x)|=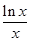 +
+ 是否有实数解,并说明理由.
是否有实数解,并说明理由.
已知Sn是等比数列{an}的前n项和,S4,S2,S3成等差数列,且a2+a3+a4=-18.
(1)求数列{an}的通项公式;
(2)是否存在正整数n,使得Sn≥2 013?若存在,求出符合条件的所有n的集合;若不存在,说明理由.
设y=(log2x)2+(t-2)log2x-t+1,若t在[-2,2]上变化时,y恒取正值,求x的取值范围.
已知椭圆C: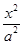 +
+ =1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,
=1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,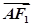 ·
· =0,3|
=0,3| |·|
|·|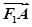 |=-5
|=-5 ·
·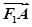 ,|
,| |=2,过点F2且与坐标轴不垂直的直线交椭圆于P,Q两点.
|=2,过点F2且与坐标轴不垂直的直线交椭圆于P,Q两点.
(1)求椭圆C的方程;
(2)线段OF2(O为坐标原点)上是否存在点M(m,0),使得 ·
· =
= ·
· ?若存在,求出实数m的取值范围;若不存在,说明理由.
?若存在,求出实数m的取值范围;若不存在,说明理由.