如图所示,在正三棱柱 中,底面边长为
中,底面边长为 ,侧棱长为
,侧棱长为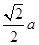 ,
, 是棱
是棱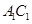 的中点.
的中点.
|
(Ⅰ)求证: 平面
平面 ;
;
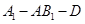 的大小;
的大小;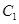 到平面
到平面 的距离.
的距离.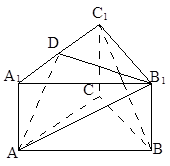
如右图所示,在△ABC中,AC=2,BC=1,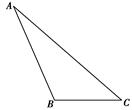
cos C=.
(1)求AB的值;
(2)求sin的值.
已知函数f(x)=sin(ωx+φ)-cos(ωx+φ),(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为.
(1)求f的值;
(2)将函数y=f(x)的图象向右平移个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的解析式及其单调递减区间
已知函数f(x)=Asin(x+φ)(A>0,0<φ<π)(x∈R)的最大值是1,其图象经过点M.
(1)求f(x)的解析式;
(2)已知α、β∈,且f(α)=,f(β)=,
求f(α-β)的值.
已知数列{an}满足,a1=1,a2=2,an+2=,n∈N.
(1)令bn=an+1-an,证明:{bn}是等比数列:
(2)求{an}的通项公式.
设曲线y=x2+x+1-ln x在x=1处的切线为l,数列{an}中,a1=1,且点(an,an+1)在切线l上.
(1)求证:数列{1+an}是等比数列,并求an;
(2)求数列{an}的前n项和Sn.