已知三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC=½AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.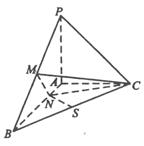
(文科)已知椭圆 :
: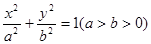 的上顶点为
的上顶点为 ,两个焦点为
,两个焦点为 、
、 ,
,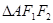 为正三角形且周长为6.
为正三角形且周长为6.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)已知圆 :
: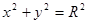 ,若直线
,若直线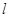 与椭圆
与椭圆 只有一个公共点
只有一个公共点 ,且直线
,且直线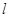 与圆
与圆 相切于点
相切于点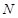 ;求
;求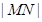 的最大值.
的最大值.
(理科)已知椭圆
 的离心率为
的离心率为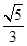 ,定点
,定点 ,椭圆短轴的端点是
,椭圆短轴的端点是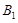 ,
,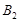 ,且
,且 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设过点 且斜率不为
且斜率不为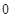 的直线交椭圆
的直线交椭圆 于
于 ,
,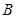 两点.试问
两点.试问 轴上是否存在定点
轴上是否存在定点 ,使
,使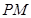 平分
平分 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(文科)给定椭圆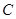 :
: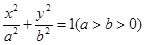 ,称圆心在原点
,称圆心在原点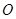 ,半径为
,半径为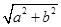 的圆是椭圆
的圆是椭圆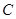 的“准圆”.若椭圆
的“准圆”.若椭圆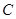 的一个焦点为
的一个焦点为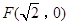 ,其短轴上的一个端点到
,其短轴上的一个端点到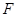 的距离为
的距离为 .
.
(Ⅰ)求椭圆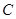 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(Ⅱ)点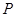 是椭圆
是椭圆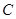 的“准圆”上的动点,过点
的“准圆”上的动点,过点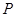 作椭圆的切线
作椭圆的切线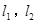 交“准圆”于点
交“准圆”于点 .
.
(ⅰ)当点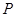 为“准圆”与
为“准圆”与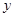 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线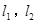 的方程并证明
的方程并证明 ;
;
(ⅱ)求证:线段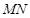 的长为定值.
的长为定值.
(理科)已知抛物线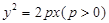 的焦点为
的焦点为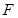 ,过
,过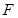 的直线交
的直线交 轴正半轴于点
轴正半轴于点 ,交抛物线于
,交抛物线于 两点,其中点
两点,其中点 在第一象限.
在第一象限.
(Ⅰ)求证:以线段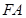 为直径的圆与
为直径的圆与 轴相切;
轴相切;
(Ⅱ)若 ,
, ,
,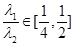 ,求
,求 的取值范围.
的取值范围.
(文科)已知椭圆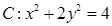 ,
,
(1)求椭圆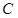 的离心率.
的离心率.
(2)设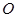 为原点,若点
为原点,若点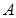 在椭圆
在椭圆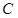 上,点
上,点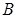 在直线
在直线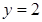 上,且
上,且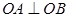 ,求直线
,求直线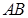 与圆
与圆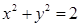 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.