甲、乙两个箱子中装有大小相同的小球,甲箱中有2个红球和2个黑球,乙箱中装有2个黑球和3个红球,现从甲箱和乙箱中各取一个小球并且交换。
(1)求交换后甲箱中刚好有两个黑球的概率。
(2)设交换后甲箱中黑球的个数为 ,求
,求 的分布列和数学期望。
的分布列和数学期望。
(本小题满分12分)
已知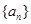 为等比数列,
为等比数列, 为等差数列
为等差数列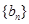 的前n项和,
的前n项和,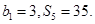
(1)求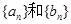 的通项公式;
的通项公式;
(2)设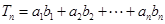 ,求
,求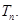
设函数 ,其中
,其中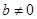 。
。
⑴当 时,判断函数
时,判断函数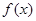 在定义域上的单调性;
在定义域上的单调性;
⑵求函数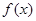 的极值点;
的极值点;
⑶证明对任意的正整数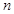 ,不等式
,不等式 成立。
成立。
如图,矩形 的两条对角线相交于点
的两条对角线相交于点 ,
,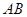 边所在直线的方程为
边所在直线的方程为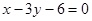 ,点
,点 在
在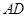 边所在直线上。
边所在直线上。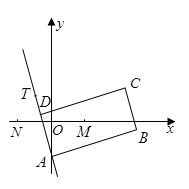
⑴求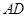 边所在直线的方程;
边所在直线的方程;
⑵求矩形 外接圆的方程;
外接圆的方程;
⑶若动圆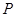 过点
过点 ,且与矩形
,且与矩形 的外接圆外切,求动圆
的外接圆外切,求动圆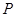 的圆心的轨迹方程。
的圆心的轨迹方程。
如图,甲船以每小时 海里的速度向正北方向航行,乙船按固定的方向匀速直线航行。当甲船位于
海里的速度向正北方向航行,乙船按固定的方向匀速直线航行。当甲船位于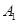 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西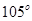 方向的
方向的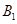 处,此时两船相距
处,此时两船相距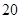 海里,当甲船航行
海里,当甲船航行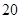 分钟到达
分钟到达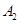 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西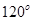 方向的
方向的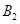 处,此时两船相距
处,此时两船相距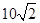 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
如图所示,在四面体 中,已知
中,已知 ,
, ,
, ,
, ,
, 是线段
是线段 上一点,
上一点, ,点
,点 在线段
在线段 上,且
上,且 。
。
⑴证明 ;
;
⑵求二面角 的平面角的正弦值。
的平面角的正弦值。