已知椭圆 经过点
经过点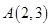 ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点 在
在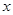 轴上,离心率
轴上,离心率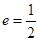 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)求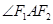 的角平分线所在直线
的角平分线所在直线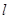 的方程;
的方程;
(Ⅲ)在椭圆 上是否存在关于直线
上是否存在关于直线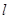 对称的相异两点?
对称的相异两点?
若存在,请找出;若不存在,说明理由.
(本小题满分13分)已知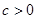 且
且 ,设
,设 :指数函数
:指数函数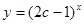 在
在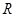 上为减函数,
上为减函数, :不等式
:不等式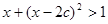 的解集为
的解集为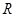 .若
.若 为假,
为假,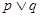 为真,求
为真,求 的取值范围.
的取值范围.
(本小题满分13分)如下图,给出了一个程序框图,其作用是输入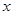 的值,输出相应的
的值,输出相应的 的值,
的值,
(I)请指出该程序框图所使用的逻辑结构;
(Ⅱ)若视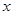 为自变量,
为自变量, 为函数值,试写出函数
为函数值,试写出函数 的解析式;
的解析式;
(Ⅲ)若要使输入的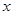 的值与输出的
的值与输出的 的值相等,则输入
的值相等,则输入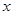 的值的集合为多少?
的值的集合为多少?
(本题满分13分)在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率.
某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩(均为整数)分成六段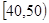 ,
,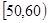 …
… 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是40~50分及90~100分的学生中选两人,记他们的成绩为x,y,求满足“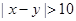 ”的概率.
”的概率.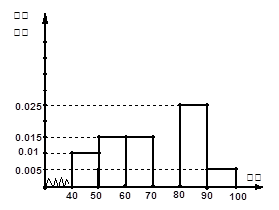
设点A为半径是1的圆O上一定点,在圆周上等可能地任取一点B.
(1)求弦AB的长超过圆内接正三角形边长的概率;
(2)求弦AB的长超过圆半径的概率.