已知二次函数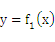
的图像的顶点为原点，且过
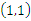，反比例函数
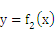的图像与直线y="x的两个交点间距离为8，已知"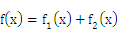 
(1)求函数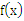
的表达式；
(2)试证明：当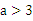
时，关于x的方程
有三个实数解。
已知椭圆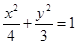
上存在两点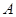
、
关于直线
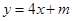对称，求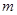
的取值范围.
某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者从装有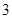
个红球、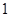
个蓝球、6个白球的袋中任意摸出4个球.根据摸出
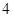个球中红球与蓝球的个数,设一、二、三等奖如下:
| 奖级 |
摸出红、蓝球个数 |
获奖金额 |
| 一等奖 |
3红1蓝 |
200元 |
| 二等奖 |
3红1白 |
50元 |
| 三等奖 |
2红1蓝或2红2白 |
10元 |
其余情况无奖且每次摸奖最多只能获得一个奖级.
(1)求一次摸奖恰好摸到1个红球的概率；
(2)求摸奖者在一次摸奖中获奖金额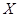
的分布列与期望
.
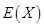求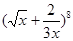
的二项展开式中的第5项的二项式系数和系数.
已知函数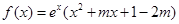
，其中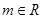
.
（Ⅰ）当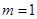
时，求函数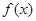
的单调递增区间；
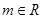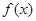（Ⅱ）证明：对任意，函数的图象在点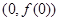
处的切线恒过定点；
（Ⅲ）是否存在实数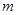
的值，使得函数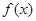在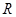
上存在最大值或最小值？若存在，求出实数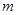的取值范围；若不存在，请说明理由.
已知某公司生产某品牌服装的年固定成本为10万元，每生产千件需另投入2.7万元，设该公司年内共生产该品牌服装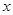
千件并全部销售完，每千件的销售收入为
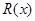万元，且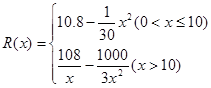
．
（Ⅰ）写出年利润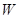
（万元）关于年产品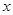（千件）的函数解析式；
（Ⅱ）年产量为多少千件时，该公司在这一品牌服装的生产中所获年利润最大？
（注：年利润=年销售收入－年总成本）