某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者从装有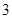
个红球、
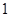个蓝球、6个白球的袋中任意摸出4个球.根据摸出
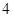个球中红球与蓝球的个数,设一、二、三等奖如下:
| 奖级 |
摸出红、蓝球个数 |
获奖金额 |
| 一等奖 |
3红1蓝 |
200元 |
| 二等奖 |
3红1白 |
50元 |
| 三等奖 |
2红1蓝或2红2白 |
10元 |
其余情况无奖且每次摸奖最多只能获得一个奖级.
(1)求一次摸奖恰好摸到1个红球的概率；
(2)求摸奖者在一次摸奖中获奖金额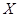
的分布列与期望
.
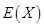中，
，设
（
），数列
满足：
．
是等差数列；
．
的通项
，求数列
．
中，内角A，B，C所对的边分别为a，b，c，已知
．
，求
”，q：“
”，若“
”是真命题，求实数a的取值范围．
经过坐标原点和点
，且与直线
相切， 从圆
向该圆引切线
，
为切点，
，且
， 试判断点
是否总在某一定直线
上，若是，求出
轴的交点为
，点
是直线
上两动点，且以
过点