求值: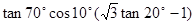
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
求证:(1)CM∥平面PAD.
(2)平面PAB⊥平面PAD.
如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,SD= AD,E为CD上一点,且CE=3DE.
AD,E为CD上一点,且CE=3DE.
(1)求证:AE⊥平面SBD.
(2)M,N分别为线段SB,CD上的点,是否存在M,N,使MN⊥CD且MN⊥SB,若存在,确定M,N的位置;若不存在,说明理由.
如图,在圆锥PO中,已知PO= ,☉O的直径AB=2,C是
,☉O的直径AB=2,C是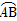 的中点,D为AC的中点.
的中点,D为AC的中点.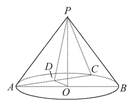
求证:平面POD⊥平面PAC.
如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.
求证:(1)BC1⊥AB1.
(2)BC1∥平面CA1D.
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F,G分别是AB,AD,CD的中点,计算: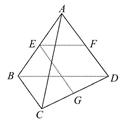
(1)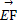 ·
· .
.
(2)EG的长.
(3)异面直线EG与AC所成角的大小.