如图，平面ABDE⊥平面ABC，AC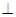
BC，AC=BC=4，四边形ABDE是直角梯形，BD
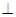AE，BDBA，AE=2BD=4，O、M分别为CE、AB的中点.
（Ⅰ）证明：OD//平面ABC；
（Ⅱ）能否在EM上找一点N，使得ON⊥平面ABDE？若能，请指出点N的位置，并加以证明；若不能，请说明理由.
已知数列{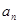
}为等差数列，公差d≠0，同{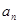}中的部分项组成的数列
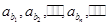为等比数列，其中
。
（1）求数列{
}的通项公式；
（2）记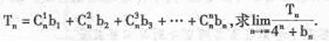
如图，在三棱锥P－ABC中，PB⊥面ABC，∠ABC＝90°，AB＝BC＝2，∠PAB＝45°，点D，E，F分别是AC，AB，BC的中点。
（1）求证：EF⊥PD；
（2）求直线PF与平面PBD所成的角的大小；
（3）求二面角E－PF－B的大小。
甲、乙两人各进行3次射击，甲每次击中目标的概率为
，乙每次击中目标的概率为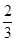
。
（1）记甲击中目标的次数为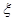
，求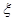的概率分布及数学期望；
（2）求乙至多击目标2次的概率；
（3）求甲恰好比乙多击中目标2次的概率。
已知向量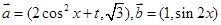
，函数f(x)＝
。
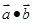（1）求函数y=f(x)的最小正周期以及单调递增区间；
（2）当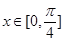
时，f(x)有最大值4，求实数t的值。
设函数
在
及
时取得极值．
（Ⅰ）求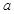
、b的值；
（Ⅱ）若对于任意的
，都有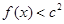
成立，求c的取值范围．