阅读下面材料:
问题:如图①,在△ABC中, D是BC边上的一点,若∠BAD=∠C=2∠DAC=45°,DC=2.求BD的长.
小明同学的解题思路是:利用轴对称,把△ADC进行翻折,再经过推理、计算使问题
得到解决.
(1)请你回答:图中BD的长为 ;
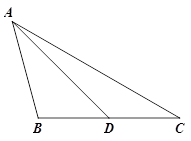
(2)参考小明的思路,探究并解答问题:如图②,在△ABC中,D是BC边上的一点,若∠BAD=∠C=2∠DAC=30°,DC=2,求BD和AB的长.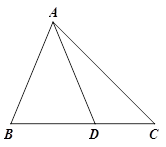
如图,⊙ O是△ ABC的外接圆, AC是直径,弦 BD= BA, EB⊥ DC,交 DC的延长线于点 E.
(1)求证: BE是⊙ O的切线;
(2)当sin∠ BCE= , AB=3时,求 AD的长.

王阿姨家的阳台上放置了一个晾衣架,完全稳固张开如图①.图②,③是晾衣架的侧面展开图,△ AOB是边长为130 cm的等边三角形,晾衣架 OE, OF能以 O为圆心转动,且 OE= OF=130 cm:在 OA, OB上的点 C, D处分别有支撑杆 CN, DM能以 C, D为圆心转动.
(1)如图②,若 EF平行于地面 AB,王阿姨的衣服穿在衣架上的总长度是110 cm,垂挂在晾衣杆 OE上是否会拖到地面上?说明理由.
(2)如图③,当支撑杆 DM支到点 M′,此时∠ EOB=78°,点 E离地面距离最大.保证衣服不拖到地面上,衣服穿在衣架上的总长度最长约为多少厘米?(结果取整)参考数据:( ,sin78°≈ ,cos78°≈ ,sin18°≈ ,cos18°≈ )

如图,在△ ABC中,∠ BAC=45°, AD⊥ BC于点 D, BD=6, DC=4,求 AD的长.小明同学利用翻折,巧妙地解答了此题,按小明的思路探究并解答下列问题:
(1)分别以 AB, AC所在直线为对称轴,画出△ ABD和△ ACD的对称图形,点 D的对称点分别为点 E, F,延长 EB和 FC相交于点 G,求证:四边形 AEGF是正方形;
(2)设 AD= x,建立关于 x的方程模型,求出 AD的长.

"金山银山,不如绿水青山".鄂尔多斯市某旗区不断推进"森林城市"建设,今春种植四类树苗,园林部门从种植的这批树苗中随机抽取了4000棵,将各类树苗的种植棵数绘制成扇形统计图,将各类树苗的成活棵数绘制成条形统计图,经统计松树和杨树的成活率较高,且杨树的成活率为97%,根据图表中的信息解答下列问题:

(1)扇形统计图中松树所对的圆心角为 度,并补全条形统计图.
(2)该旗区今年共种树32万棵,成活了约多少棵?
(3)园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用 A, B, C, D表示)
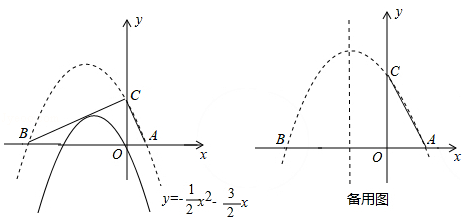
已知抛物线 y=﹣ x 2﹣ x的图象如图所示:
(1)将该抛物线向上平移2个单位,分别交 x轴于 A、 B两点,交 y轴于点 C,则平移后的解析式为 .
(2)判断△ ABC的形状,并说明理由.
(3)在抛物线对称轴上是否存在一点 P,使得以 A、 C、 P为顶点的三角形是等腰三角形?若存在,求出点 P的坐标;若不存在,说明理由.