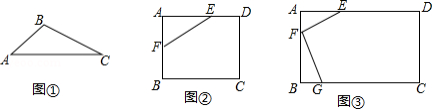
已知如图，在△ABC中，ABAC，∠ABCα，将△ABC以点-优题课

已知如图，在△ABC中，AB=AC，∠ABC=α，将△ABC以点B为中心，沿逆时针方向旋转α度（0°＜α＜90°），得到△BDE，点B、A、E恰好在同一条直线上，连结CE.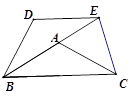

（1）则四边形DBCE是_______形（填写：平行四边形、矩形、菱形、正方形、梯形）
（2）若AB=AC=1，BC=，请你求出四边形DBCE的面积.

科目数学题型解答题难度中等

知识点：解直角三角形

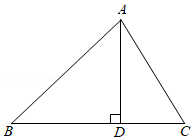
小军学校门前有座山，山顶上有一观景台，他很想知道这座山比他们学校的旗杆能高出多少米．于是，有一天，他和同学小亮带着测倾器和皮尺来到观景台进行测量．测量方案如下：如图，首先，小军站在观景台的 $C$ 点处，测得旗杆顶端 $m$ 点的俯角为 $35 °$ ，此时测得小军眼睛距 $C$ 点的距离 $BC$ 为1.8米；然后，小军在 $C$ 点处蹲下，测得旗杆顶端 $M$ 点的俯角为 $34.5 °$ ，此时测得小军的眼睛距 $C$ 点的距离 $AC$ 为1米．请根据以上所测得的数据，计算山 $CD$ 比旗杆 $MN$ 高出多少米（结果精确到1米）？

（参考数据： $\sin 35 ° \approx 0.5736$ ， $\cos 35 ° \approx 0.8192$ ， $\tan 35 ° \approx 0.7002$ ， $\sin 34.5 ° \approx 0.5664$ ， $\cos 34.5 ° \approx 0.8241$ ， $\tan 34.5 ° \approx 0.6873)$

如图，在 $▱ ABCD$ 中，延长 $BA$ 到点 $E$ ，延长 $DC$ 到点 $F$ ，使 $AE = CF$ ，连接 $EF$ 交 $AD$ 边于点 $G$ ，交 $BC$ 边于点 $H$ ．求证： $DG = BH$ ．

“垃圾不落地，城市更美丽”．某中学为了了解七年级学生对这一倡议的落实情况，学校安排政教处在七年级学生中随机抽取了部分学生，并针对学生“是否随手丢垃圾”这一情况进行了问卷调查，统计结果为： $A$ 为从不随手丢垃圾； $B$ 为偶尔随手丢垃圾； $C$ 为经常随手丢垃圾三项．要求每位被调查的学生必须从以上三项中选一项且只能选一项，现将调查结果绘制成以下两幅不完整的统计图．

请你根据以上信息，解答下列问题：

（1）补全上面的条形统计图和扇形统计图；

（2）所抽取学生“是否随手丢垃圾”情况的众数是　　；

（3）若该校七年级共有1500名学生，请你估计该年级学生中“经常随手丢垃圾”的学生约有多少人？谈谈你的看法？

如图，在 $ΔABC$ 中， $AD$ 是 $BC$ 边上的高．请用尺规作图法在高 $AD$ 上求作一点 $P$ ，使得点 $P$ 到 $AB$ 的距离等于 $PD$ 的长．（保留作图痕迹，不写作法）

问题提出

（1）如图①，已知 $ΔABC$ ，请画出 $ΔABC$ 关于直线 $AC$ 对称的三角形．

问题探究

（2）如图②，在矩形 $ABCD$ 中， $AB = 4$ ， $AD = 6$ ， $AE = 4$ ， $AF = 2$ ，是否在边 $BC$ 、 $CD$ 上分别存在点 $G$ 、 $H$ ，使得四边形 $EFGH$ 的周长最小？若存在，求出它周长的最小值；若不存在，请说明理由．

问题解决

（3）如图③，有一矩形板材 $ABCD$ ， $AB = 3$ 米， $AD = 6$ 米，现想从此板材中裁出一个面积尽可能大的四边形 $EFGH$ 部件，使 $∠ EFG = 90 °$ ， $EF = FG = \sqrt{5}$ 米， $∠ EHG = 45 °$ ，经研究，只有当点 $E$ 、 $F$ 、 $G$ 分别在边 $AD$ 、 $AB$ 、 $BC$ 上，且 $AF < BF$ ，并满足点 $H$ 在矩形 $ABCD$ 内部或边上时，才有可能裁出符合要求的部件，试问能否裁得符合要求的面积尽可能大的四边形 $EFGH$ 部件？若能，求出裁得的四边形 $EFGH$ 部件的面积；若不能，请说明理由．