已知数列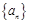 单调递增,且各项非负,对于正整数
单调递增,且各项非负,对于正整数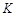 ,若任意的
,若任意的 ,
, (
(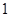 ≤
≤ ≤
≤ ≤
≤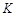 ),
), 仍是
仍是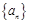 中的项,则称数列
中的项,则称数列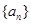 为“
为“ 项可减数列”.
项可减数列”.
(1)已知数列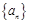 是首项为2,公比为2的等比数列,且数列
是首项为2,公比为2的等比数列,且数列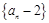 是“
是“ 项可减数
项可减数
列”,试确定 的最大值;
的最大值;
(2)求证:若数列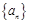 是“
是“ 项可减数列”,则其前
项可减数列”,则其前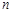 项的和
项的和 ;
;
(3)已知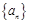 是各项非负的递增数列,写出(2)的逆命题,判断该逆命题的真假,
是各项非负的递增数列,写出(2)的逆命题,判断该逆命题的真假,
并说明理由.
椭圆E的中心在坐标原点O,焦点在x轴上,离心率为 .点P(1,
.点P(1, )、A、B在椭圆E上,且
)、A、B在椭圆E上,且 +
+ =m
=m (m∈R).
(m∈R).
(1)求椭圆E的方程及直线AB的斜率;
(2)求证:当△PAB的面积取得最大值时,原点O是△PAB的重心.
如图,已知E,F分别是正方形ABCD边BC、CD的中点,EF与AC交于点O,PA,NC都垂直于平面ABCD,且PA=AB=4,NC=2,M是线段PA上的一动点.
(1)求证:平面PAC⊥平面NEF;
(2)若PC∥平面MEF,试求PM∶MA的值;
(3)当M的是PA中点时,求二面角M-EF-N的余弦值.
南昌市教育局组织中学生足球比赛,共有实力相当的8支代表队(含有一中代表队,二中代表队)参加比赛,比赛规则如下:
第一轮:抽签分成四组,每组两队进行比赛,胜队进入第二轮,第二轮:将四队分成两组,每组两队进行比赛,胜队进入第三轮,第三轮:两队进行决赛,胜队获得冠军。
现记ξ=0表示整个比赛中一中代表队与二中代表队没有相遇,ξ=i表示恰好在第i轮比赛时一中代表队,二中代表队相遇(i=1,2,3).
(1)求ξ的分布列;
(2)求Eξ.
已知各项均不相等的等差数列{an}的前四项和S4=14,且a1,a3,a7成等比数列.
(1)求数列{an}的通项公式;
(2)设Tn为数列{ }的前n项和,若Tn≤λan+1对∀n∈N*恒成立,求实数λ的最小值.
}的前n项和,若Tn≤λan+1对∀n∈N*恒成立,求实数λ的最小值.
已知向量p=(-cos 2x,a),q=(a,2- sin 2x),函数f(x)=p·q-5(a∈R,a≠0)
sin 2x),函数f(x)=p·q-5(a∈R,a≠0)
(1)求函数f(x)(x∈R)的值域;
(2)当a=2时,若对任意的t∈R,函数y=f(x),x∈(t,t+b]的图像与直线y=-1有且仅有两个不同的交点,试确定b的值(不必证明),并求函数y=f(x)的在[0,b]上单调递增区间.