一种放射性元素，最初的质量为500g，按每年10﹪衰减.
（Ⅰ）求t年后，这种放射性元素质量ω的表达式；
（Ⅱ）由求出的函数表达式，求这种放射性元素的半衰期（剩留量为原来的一半所需要的时间）．（精确到0.1；参考数据：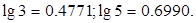
）
（本小题满分10）已知
．
（1）求
的值；
（2）求
的值．
（本小题共14分）已知定义在
上的函数
（1）求证：
存在唯一的零点，且零点属于（3，4）；
（2）若
，且
对任意的
1恒成立，求
的最大值.
（本小题共13分）已知椭圆
的左焦点为
，过点M（-3，0）作一条斜率大于0的直线
与W交于不同的两点A、B，延长BF交W于点C.
（1）求椭圆W的离心率；
（2）求证：点A与点C关于
轴对称.
（本小题共13分）设
，已知函数
.
（1）当
时，求函数
的单调区间；
（2）若对任意的
，有
恒成立，求实数
的取值范围.
（本小题共14分）如图，将矩形ABCD沿对角线BD把△ABD折起，使A点移到
点，且在平面BCD上的射影O恰好在CD上.
（1）求证：BC⊥
；
（2）求证：平面
⊥平面
；
（3）若AB=10，BC=6，求三棱锥
的体积.