如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点,P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．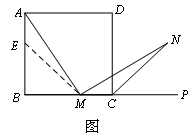
下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
证明：在边AB上截取AE=MC，连ME．
正方形ABCD中，∠B=∠BCD=90°，AB=BC．
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE．
（下面请你完成余下的证明过程）
（2）若将(1)中的“正方形ABCD”改为“正三角形ABC”（如图2）,N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．
（3）若将（1）中的“正方形ABCD”改为“正
边形ABCD…X”，请你作出猜想：当∠AMN= °时，结论AM=MN仍然成立．
（直接写出答案，不需要证明）
（本题10分）如图，直线AB与CD相交于O，OE⊥AB，OF⊥CD,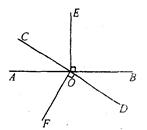 
（1）图中与∠COE互余的角是______________；图中与∠COE互补的角是______________；（把符合条件的角都写出来）
（2）如果∠AOC＝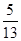
∠EOF,求∠AOC的度数．
（本题10分）元旦期间，七（1）班的小明、小丽等同学随家长一行共12人同到某公园游玩，小明爸爸根据贴在公园门口的下表购买了成人票和学生票共花去350元。
（1）小明他们一共去了几个成人，几个学生？
（2）请你帮助小明爸爸想一想，购买门票有更省钱的方式吗？如果有，怎么买？说明理由。
| 成人票 |
学生票 |
团体票（16人以上含16人） |
|
| 票价 |
35元/ 张 |
17.5元/ 张 |
21元/ 张 |
（本题10分）如图,已知同一平面内∠AOB=90o,∠AOC=60o，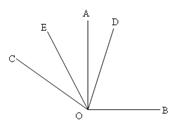
（1）填空∠BOC =；
（1）如OD平分∠BOC，OE平分∠AOC，直接写出∠DOE的度数为°；
（3）试问在（2）的条件下，如果将题目中∠AOC=60o改成∠AOC=2α（α<45o），其他条件不变，你能求出∠DOE的度数吗？若能，请你写出求解过程；若不能，请说明理由．
（本题10分）如图，由相同边长的小正方形组成的网格图形，A、B、C都在格点上．
（1）过点C画直线AB的平行线；
（2）过点A画直线BC的垂线，并注明垂足为点G；过点A画直线AB的垂线，交BC于点H．
（3）线段AH的长度是点到直线的距离．
（4）线段AG、AH的大小关系为：AGAH（填“>”或“<”或“=”），理由是。
（本题10分）如图，线段AB=8cm，C是线段AB上一点，AC=3cm，M是AB的中点， N是AC的中点．
（1）求线段CM的长；
（2）求线段MN的长．