如图,甲船以每小时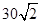
海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于
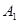处时,乙船位于甲船的北偏西
的方向
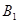处,此时两船相距20海里.当甲船航行20分钟到达
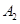处时,乙船航行到甲船的北偏西
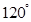方向的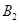
处,此时两船相距
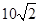海里,问乙船每小时航行多少海里?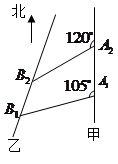
已知函数f（x）=|2x+1|-|x-3|．
（Ⅰ）解不等式f（x）≤4；
（Ⅱ）若存在x使得f（x）+a≤0成立，求实数a的取值范围．
双曲线C与椭圆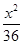
+
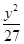=1有相同焦点，且经过点（4，
）．
（1）求双曲线的方程；
（2）若F1，F2是双曲线C的两个焦点，点P在双曲线C上，且∠F1PF2=60°，求△F1PF2的面积．
如图，PA⊥平面ABCD，矩形ABCD的边长AB=1，BC=2，E为BC的中点．
（1）证明：PE⊥DE；
（2）如果PA=2，求异面直线AE与PD所成的角的大小．
已知直线l：3x+4y-2=0
（Ⅰ）求经过直线l与直线x+3y-4=0的交点P，且垂直于直线x-2y-1=0的方程；
（Ⅱ）求直线l与两坐标轴围成的三角形的内切圆的方程．
（本小题满分14分）已知函数
，其中
．
（1）求
的单调区间；
（2）求证：
＜