(本小题满分12分)
在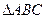 中,角A、B、C所对边分别是a、b、c,
中,角A、B、C所对边分别是a、b、c,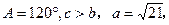
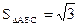 ,求
,求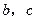 .
.
(本小题满分12分)
设有两个命题p:关于x的不等式 (a > 0,且a ≠ 1)的解集是{ x |
(a > 0,且a ≠ 1)的解集是{ x |  x < 0 };
x < 0 };
q:函数 的定义域为R.如果
的定义域为R.如果 为真命题,
为真命题, 为假命题,
为假命题,
求实数a的取值范围.
(本小题满分10分)
已知: 函数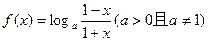 ,
,
(1)求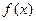 的定义域;
的定义域;
(2)解关于x的不等式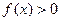 .
.
设数列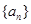 的前
的前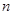 项和为
项和为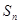 , 已知
, 已知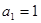 ,
,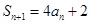 .
.
(1)设 ,证明数列
,证明数列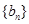 是等比数列;
是等比数列;
(2)求数列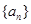 的通项公式;
的通项公式;
(3)设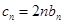 ,求数列
,求数列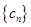 的前n项和
的前n项和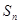 .
.
(.(本小题满分12分)
如图,四棱锥S-ABCD的底面是矩形,AB a,AD
a,AD 2,SA
2,SA 1,且SA⊥底面ABCD,若
1,且SA⊥底面ABCD,若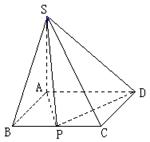
边BC上存在异于B,C的一点P,使得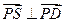 .
.
(1)求a的最大值;
(2)当a取最大值时,求平面SCD的一 个单位法向量
个单位法向量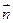
及点P到平面SCD的距离.