如图 5，已知正方形ABCD在水平面上的正投影（投影线垂直于投影面）是四边形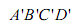
，其中A与A '重合，且BB'＜DD'＜CC'．
（1）证明AD'//平面BB'C'C，并指出四边形AB'C'D’的形状；
（2）如果四边形中AB'C'D’中，
，正方形的边长为
，
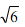求平面ABCD与平面AB'C'D’所成的锐二面角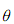
的余弦值．
( 14分)
已知椭圆C的中心为直角坐标系x0y的原点，焦点在
轴上，它的一个项点到两个焦点的距离分别是7和1
(1)求椭圆C的方程
(2)若
为椭圆C的动点，M为过P且垂直于轴的直线上的点，
（e为椭圆C的离心率），求点M的轨迹方程，并说明轨迹是什么曲线。
已知椭圆中心在原点，焦点在
x轴上，长轴长等于12，离心率为
.
（Ⅰ）求椭圆的标准方程；
（Ⅱ
）过椭圆左顶点作直线l垂直于x轴
，若动点M到椭圆右焦点的距离比它到直线l的距离小4，求点M的轨迹方程.
过抛物线y2＝4x的焦点F作直线l，交抛物线于A、B两点，若线段AB的中点的横坐标为3，求|AB|
（1）求抛物线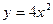
在点（1,4）处的切线方程
（2）求曲线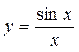
在点M(π，0)处的切线的斜率
求双曲线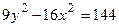
的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程。