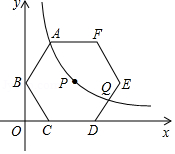
如图,在ΔABC中,点O是AC边上的一个动点,过点O作直线MN//BC,∠ACB以及外角∠ACD的平分线分别交MN于点E、F。求证OE=OF
当点O运动到AC边的什么位置时,四边形AECF是矩形?回答并证明你的结论。
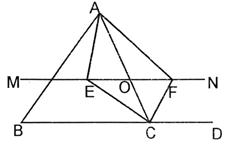
图1,图2都是由边长为1的小等边三角形构成的网格,每个网格图中有5个小等边三角形已涂上阴影,请在余下的空白小等边三角形中,按下列要求选取一个涂上阴影:
(1)使得6个阴影小等边三角形组成一个轴对称图形.
(2)使得6个阴影小等边三角形组成一个中心对称图形.
(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
先化简,再求值: ,其中 .
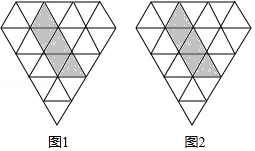
如图,在等腰 中, , ,点 , 分别在边 , 上,将线段 绕点 按逆时针方向旋转 得到 .
(1)如图1,若 ,点 与点 重合, 与 相交于点 .求证: .
(2)已知点 为 的中点.
①如图2,若 , ,求 的长.
②若 ,是否存在点 ,使得 是直角三角形?若存在,求 的长;若不存在,试说明理由.
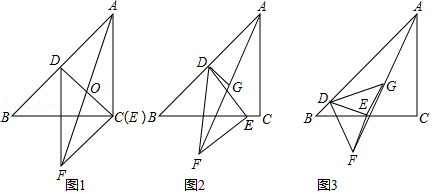
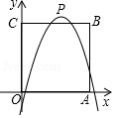
如图,在平面直角坐标系中,正方形 的边长为4,边 , 分别在 轴, 轴的正半轴上,把正方形 的内部及边上,横、纵坐标均为整数的点称为好点.点 为抛物线 的顶点.
(1)当 时,求该抛物线下方(包括边界)的好点个数.
(2)当 时,求该抛物线上的好点坐标.
(3)若点 在正方形 内部,该抛物线下方(包括边界)恰好存在8个好点,求 的取值范围.
如图,在平面直角坐标系中,正六边形 的对称中心 在反比例函数 的图象上,边 在 轴上,点 在 轴上,已知 .
(1)点 是否在该反比例函数的图象上?请说明理由;
(2)若该反比例函数图象与 交于点 ,求点 的横坐标;
(3)平移正六边形 ,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.