如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E,点F在BD上,连接AF、EF.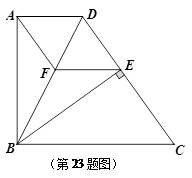
求证:DA=DE;
如果AF∥CD,求证:四边形ADEF是菱形.
探究
如图①,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,连结AC、EF.在图中找一个与△FAE全等的三角形,并加以证明.
应用
以□ABCD的四条边为边,在其形外分别作正方形,如图②,连结EF、GH、IJ、KL.若□ABCD的面积为5,则图中阴影部分四个三角形的面积和为.
如图,平面直角坐标系中,抛物线
交
轴于点
,
为抛物线
上一点,且与点
不重合.连结
,以
,
为邻边作
,
所在直线与
轴交
于点
.设点P的横坐标为
.
(1)点
落在
轴上时
的值.
(3)若点
在
轴下方,则
为何值时,线段
的长取最大值,并求出这个最大值.[参考公式:二次函数
的顶点坐标为
]
某校课外兴趣小组从我市七年级学生中抽取2 000人做了如下问卷调查,将统计
结果绘制了如下两幅统计图.

根据上述信息解答下列问题:
(1)求条形统计图中n的值.
(2)如果每瓶饮料平均3元钱,“少2瓶以上”按少喝3瓶计算.
①求这2000名学生一个月少喝饮料能节省多少钱捐给希望工程?
②按上述统计结果估计,我市七年级6万学生一个月少喝饮料大约能节省多少钱捐给希望工程?
如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),
AB= .
.
(1)求⊙P的半径.
(2)将⊙P向下平移,求⊙P与x轴相切时平移的距离.
在正方形网格图①、图②中各画一个等腰三角形.每个等腰三角形的一个顶点为
格点A,其余顶点从格点B、C、D、E、F、G、H中选取,并且所画的两个三角形不全等.