设函数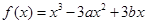 的图像与直线
的图像与直线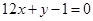 相切于点
相切于点 .
.
(1)求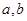 的值;(2)讨论函数
的值;(2)讨论函数 的单调性.
的单调性.
(本小题满分12分)如图,已知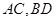 是圆
是圆 的两条互相垂直的直径,直角梯形
的两条互相垂直的直径,直角梯形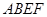 所在平面与圆
所在平面与圆 所在平面互相垂直,其中
所在平面互相垂直,其中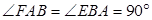 ,
, ,
,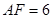 ,
, ,点
,点 为线段
为线段 中点.
中点.
(Ⅰ)求证:直线 平面
平面 ;
;
(Ⅱ)若点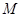 在线段
在线段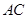 上,且点
上,且点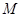 在平面
在平面 上的射影为线段
上的射影为线段 的中点,请求出线段
的中点,请求出线段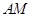 的长.
的长.
(本小题满分12分)某运动队拟在2015年3月份安排5次体能测试,规定:依次测试,只需有一次测试合格就不必参加后续的测试.已知运动员小刘5次测试每次合格的概率依次构成一个公差为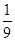 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过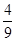 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为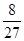 .
.
(Ⅰ)求小刘第一次参加测试就合格的概率;
(Ⅱ)在小刘参加第一、第二次测试均不合格的前提下,记小刘参加后续测试的次数为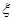 ,求随机变量
,求随机变量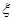 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
已知在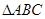 中,角
中,角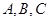 所对的边分别为
所对的边分别为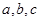 ,
, ,且
,且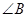 为钝角.
为钝角.
(Ⅰ)求角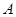 的大小;
的大小;
(Ⅱ)若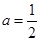 ,求
,求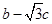 的取值范围.
的取值范围.
已知顶点为原点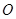 的抛物线
的抛物线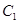 的焦点
的焦点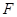 与椭圆
与椭圆 的右焦点重合
的右焦点重合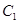 与
与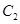 在第一和第四象限的交点分别为
在第一和第四象限的交点分别为 .
.
(1)若△AOB是边长为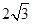 的正三角形,求抛物线
的正三角形,求抛物线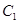 的方程;
的方程;
(2)若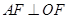 ,求椭圆
,求椭圆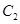 的离心率
的离心率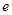 ;
;
(3)点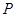 为椭圆
为椭圆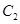 上的任一点,若直线
上的任一点,若直线 、
、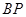 分别与
分别与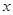 轴交于点
轴交于点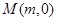 和
和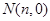 ,证明:
,证明: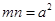 .
.
【改编】(本小题满分14分)已知函数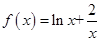 .
.
(1)求函数的单调增区间;
(2)若 ,求实数
,求实数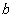 的取值范围.
的取值范围.