Rt△ABC与Rt△FED是两块全等的含30o、60o角的三-优题课

Rt△ABC与Rt△FED是两块全等的含30^o、60^o角的三角板，按如图（一）所示拼在一起，CB与DE重合．
求证：四边形ABFC为平行四边形
取BC中点O，将△ABC绕点O顺时针方向旋转到如图（二）中△位置，直线与AB、CF分别相交于P、Q两点，猜想OQ、OP长度的大小关系，并证明你的猜想．
在(2)的条件下,指出当旋转角为多少度时,四边形PCQB为菱形(不要求证明).

科目数学题型解答题难度中等

知识点：圆内接四边形的性质

某校准备组建"校园安全宣传队"，每班有两个队员名额，七年2班有甲、乙、丙、丁四位同学报名，这四位同学综合素质都很好，王老师决定采取抽签的方式确定人选．具体做法是：将甲、乙、丙、丁四名同学分别编号为1、2、3、4号，将号码分别写在4个大小、质地、形状、颜色均无差别的小球上，然后把小球放入不透明的袋子中，充分搅拌均匀后，王老师从袋中随机摸出两个小球，根据小球上的编号确定本班"校园安全宣传员"人选．

（1）用画树状图或列表法，写出"王老师从袋中随机摸出两个小球"可能出现的所有结果．

（2）求甲同学被选中的概率．

由于疫情的影响，学生不能返校上课，某校在直播授课的同时还为学生提供了四种辅助学习方式： $A$ 网上自测， $B$ 网上阅读， $C$ 网上答疑， $D$ 网上讨论．为了解学生对四种学习方式的喜欢情况，该校随机抽取部分学生进行问卷调查，规定被调查学生从四种方式中选择自己最喜欢的一种，根据调查结果绘制成如图两幅不完整的统计图：

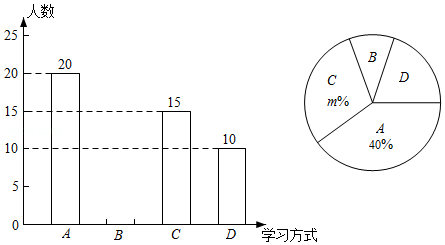
根据统计图提供的信息，解答下列问题：

（1）本次共调查了　　名学生；

（2）在扇形统计图中， $m$ 的值是　　， $D$ 对应的扇形圆心角的度数是　　；

（3）请补全条形统计图；

（4）若该校共有2000名学生，根据抽样调查的结果，请你估计该校最喜欢方式 $D$ 的学生人数．

先化简，再求值： $(\frac{x - 1}{x + 1} + 1) \div \frac{x^{3} - 2 x^{2} + x}{x^{2} - 1}$ ，其中 $x = \sqrt{3} + 1$ ．

在平面直角坐标系中，抛物线 $y = a x^{2} + bx + 2 (a \neq 0)$ 经过点 $A (- 2, - 4)$ 和点 $C (2, 0)$ ，与 $y$ 轴交于点 $D$ ，与 $x$ 轴的另一交点为点 $B$ ．

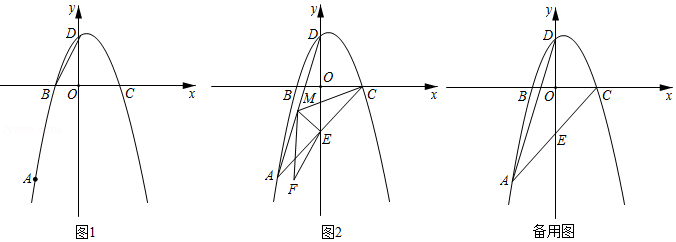
（1）求抛物线的解析式；

（2）如图1，连接 $BD$ ，在抛物线上是否存在点 $P$ ，使得 $∠ PBC = 2 ∠ BDO$ ？若存在，请求出点 $P$ 的坐标；若不存在，请说明理由；

（3）如图2，连接 $AC$ ，交 $y$ 轴于点 $E$ ，点 $M$ 是线段 $AD$ 上的动点（不与点 $A$ ，点 $D$ 重合），将 $ΔCME$ 沿 $ME$ 所在直线翻折，得到 $ΔFME$ ，当 $ΔFME$ 与 $ΔAME$ 重叠部分的面积是 $ΔAMC$ 面积的 $\frac{1}{4}$ 时，请直接写出线段 $AM$ 的长．

在矩形 $ABCD$ 中，点 $E$ 是射线 $BC$ 上一动点，连接 $AE$ ，过点 $B$ 作 $BF ⊥ AE$ 于点 $G$ ，交直线 $CD$ 于点 $F$ ．

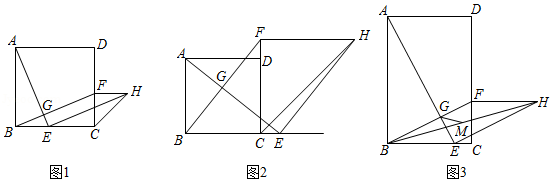
（1）当矩形 $ABCD$ 是正方形时，以点 $F$ 为直角顶点在正方形 $ABCD$ 的外部作等腰直角三角形 $CFH$ ，连接 $EH$ ．

①如图1，若点 $E$ 在线段 $BC$ 上，则线段 $AE$ 与 $EH$ 之间的数量关系是　　，位置关系是　　；

②如图2，若点 $E$ 在线段 $BC$ 的延长线上，①中的结论还成立吗？如果成立，请给予证明；如果不成立，请说明理由；

（2）如图3，若点 $E$ 在线段 $BC$ 上，以 $BE$ 和 $BF$ 为邻边作平行四边形 $BEHF$ ， $M$ 是 $BH$ 中点，连接 $GM$ ， $AB = 3$ ， $BC = 2$ ，求 $GM$ 的最小值．