如图,从 , , , , , ,这6个点中随机选取3个点。
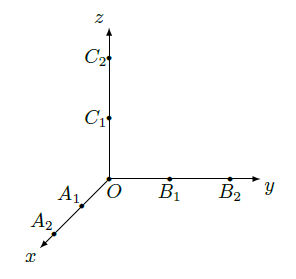
(Ⅰ)求这3点与原点 恰好是正三棱锥的四个顶点的概率;
(Ⅱ)求这3点与原点
共面的概率。
若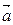 =
=
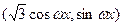 ,
,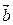 =
=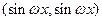 ,其中
,其中 >0,记函数f(
>0,记函数f( x)=2
x)=2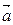 ·
·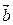 ,f(x)图象中相邻两条对称轴间的距离为
,f(x)图象中相邻两条对称轴间的距离为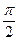 ,(1)求
,(1)求 的值;
的值;
(2)求f(x)的单调减区间和f(x)的最大值及取得最大值时x的取值集合.
在△ABC中,已知 ,c=1,
,c=1,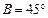 ,求a,A,C.
,求a,A,C.
在数列 中,
中,
(I)设 ,求数列
,求数列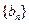 的通项公式
的通项公式
(II)求数列 的前
的前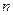 项和
项和
如图,甲船以每小时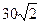 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,当甲船航行
海里,当甲船航行 分钟到达
分钟到达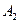 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的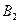 处,此时两船相距
处,此时两船相距 海里,问乙船每小时航行多少海里?(结论保留最简根式形式)
海里,问乙船每小时航行多少海里?(结论保留最简根式形式)
某市现有住房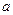
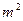 ,预计以后的10年中,人口的年增长率为
,预计以后的10年中,人口的年增长率为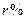 ,要想10年后
,要想10年后
人均住房面积达到现有的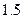 倍,试问这10年中,平均每年新建住房多少
倍,试问这10年中,平均每年新建住房多少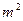 ?
?