(本小题满分14分)已知向量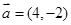 ,
,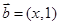 .
.
(I) 若 ,
, 共线,求
共线,求 的值;
的值;
(II)当 时,求
时,求 与
与 夹角
夹角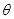 的余弦值.
的余弦值.
(本小题12分)
已知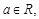 函数
函数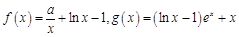
(1)判断函数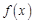 在
在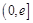 上的单调性;
上的单调性;
(2)是否存在实数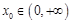 ,使曲线
,使曲线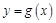 在点
在点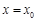 处的切线与
处的切线与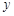 轴垂直?若存在,求出
轴垂直?若存在,求出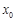 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题12分)
如图,抛物线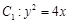 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为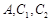 在第一象限的交点为
在第一象限的交点为 为坐标原点,且
为坐标原点,且 的面积为
的面积为

(1)求椭圆 的标准方程;
的标准方程;
(2)过点 作直线
作直线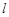 交
交 于
于 两点,射线
两点,射线 分别交
分别交 于
于 两点.
两点.
(I)求证: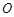 点在以
点在以 为直径的圆的内部;
为直径的圆的内部;
(II)记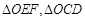 的面积分别为
的面积分别为 ,问是否存在直线
,问是否存在直线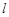 ,使得
,使得 ?请说明理由.
?请说明理由.
(本小题12分)
如图,在三棱锥 中,
中,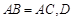 为
为 的中点,
的中点, 平面
平面 ,垂足
,垂足 落在线段
落在线段 上,已知
上,已知
(1)证明: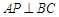 ;
;
(2)在线段 上是否存在点
上是否存在点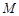 ,使得二面角
,使得二面角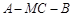 为直二面角?若存在,求出
为直二面角?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. 
(本小题12分)
随机调查某社区80个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别有关系,得到下面的数据表:
| 休闲方式 性别 |
看电视 |
看书 |
合计 |
| 男 |
10 |
50 |
60 |
| 女 |
10 |
10 |
20 |
| 合计 |
20 |
60 |
80 |
(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量 ,求
,求 的分布列和期望;
的分布列和期望;
(2)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
参考公式: 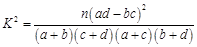 ,其中
,其中
参考数据:
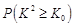 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
 |
2.072 |
2.706 |
3.841 |
5.042 |
6.635 |
(本小题12分)
已知在 中,角
中,角 所对的边分别为
所对的边分别为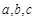 ,且
,且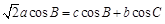
(1)求角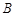 的大小;
的大小;
(2)设向量 ,求当
,求当 取最大值时,
取最大值时, 的值.
的值.