某校在两个班进行教学方式对比试验,两个月后进行了一次检测,试验班与对照班成绩统计如 列联表所示(单位:人).
列联表所示(单位:人).
| |
80及80分以上 |
80分以下 |
合计 |
| 试验班 |
35 |
15 |
50 |
| 对照班 |
20 |
 |
50 |
| 合计 |
55 |
45 |
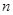 |
(1)求 ,
,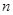 ;
;
(2)你有多大把握认为“教学方式与成绩有关系”?
参考公式及数据: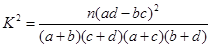 ,
,
其中 为样本容量.
为样本容量.
 |
… |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
… |
 |
… |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
… |
已知函数f (x )=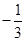 ax 3 + x2 + 2( a ≠ 0 ) .
ax 3 + x2 + 2( a ≠ 0 ) .
(Ⅰ) 试讨论函数f (x )的单调性;
(Ⅱ) 若a>0,求函数f (x ) 在[1,2]上的最大值.
在等比数列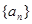 中,
中,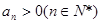 ,公比
,公比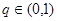 ,且
,且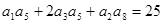 ,
,
又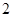 是
是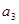 与
与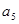 的等比中项。设
的等比中项。设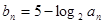 .
.
(Ⅰ) 求数列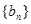 的通项公式;
的通项公式;
(Ⅱ) 已知数列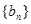 的前
的前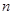 项和为
项和为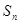 ,
,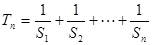 ,求
,求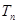 .
.
已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.
现从该箱中任取 ( 无放回 ) 3个球,记随机变量X为取出3球所得分数之和.
(Ⅰ) 求X的分布列;
(Ⅱ) 求X的数学期望E(X).
已知钝角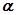 的顶点在原点,始边与
的顶点在原点,始边与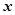 轴的正半轴重合,终边与单位圆相交于点
轴的正半轴重合,终边与单位圆相交于点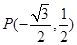 .
.
(Ⅰ) 求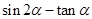 的值;
的值;
(Ⅱ) 若函数 , 试问该函数
, 试问该函数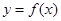 的图象可由
的图象可由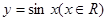 的图象经过怎样的平移和伸缩变换得到.
的图象经过怎样的平移和伸缩变换得到.
已知△ABC的内角A、B、C的对边分别为a、b、c,若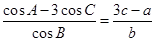 .
.
(Ⅰ) 求 的值;
的值;
(Ⅱ) 若b =2,且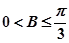 ,求边长a的取值范围.
,求边长a的取值范围.