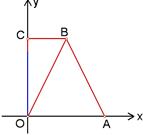
在直角梯形OABC中,CB//OA,∠COA=90°,CB=3,OA=6,BA=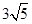 .分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.
.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.求点B的坐标;
已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;
点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
如图,直角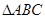 中,
中,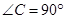 ,
,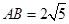 ,
,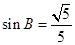 ,点
,点 为边
为边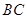 上一动点,
上一动点,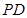 ∥
∥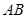 ,
,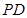 交
交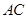 于点
于点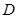 ,连结
,连结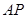 .
.
(1)求
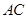 、
、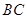 的长;
的长;(2)设
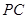 的长为
的长为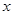 ,
,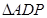 的面积为
的面积为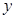 .当
.当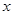 为何值时,
为何值时,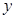 最大,并求出最大值.
最大,并求出最大值.
在平面直角坐标系xOy中,反比例函数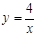 的图象与抛物线
的图象与抛物线
交于点A(3, n). 求n的值及抛物线的解析式;
过点A作直线BC,交x轴于点B,交反比例函数
 (
( )的图象于点C,且AC=2AB,求B、C两点的坐标;
)的图象于点C,且AC=2AB,求B、C两点的坐标;在(2)的条件下,若点P是抛物线对称轴上的一点,且点P到x轴和直线BC的距离相等,求点P的坐标.
如图,已知每个小方格都是边长为1的正方形,我们称每个小正方形的顶点为格点,
以格点为顶点的图形称为格点图形. 图中的△ABC是一个格点三角形.
请你在第一象限内画出格点△AB1C1, 使得△AB1C1∽△ABC,且△AB1C1与△ABC的相似比为3:1;
写出B1、C1两点的坐标.
如图一,在△ABC中,分别以AB,AC为直径在△ABC外作半圆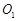 和半圆
和半圆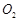 ,其中
,其中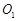 和
和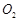 分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点.
分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点. 连结
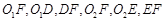 ,证明:
,证明: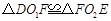 ;
;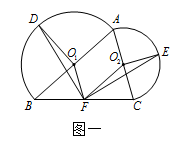
如图二,过点A分别作半圆
 和半圆
和半圆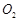 的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;
的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;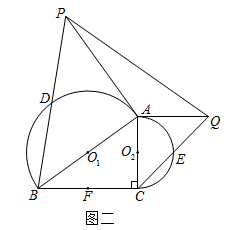
如图三,过点A作半圆
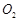 的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆
的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆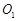 的切线.
的切线.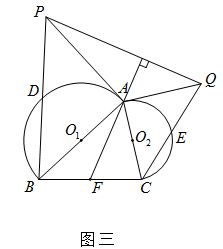
如图一,AB是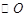 的直径,AC是弦,直线EF和
的直径,AC是弦,直线EF和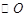 相切与点C,
相切与点C,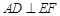 ,垂足为D.
,垂足为D.求证
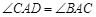 ;
;
如图二,若把直线EF向上移动,使得EF与
 相交于G,C两点(点C在点G的右侧),连结AC,AG,若题中其他条件不变,这时图中是否存在与
相交于G,C两点(点C在点G的右侧),连结AC,AG,若题中其他条件不变,这时图中是否存在与 相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由.
相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由.