如图,直线l与⊙O相交于A,B两点,且与半径OC垂直,垂足为H,已知AB=16厘米, .
.
(1) 求⊙O的半径;
(2) 如果要将直线l向下平移到与⊙O相切的位置,
平移的距离应是多少?请说明理由.
丹东市为了治理城市污水,需要铺设一段全长为300米的污水排放管道,铺设120米后,为了尽可能减少施工对城市交通所造成的影响,后来每天的工作量比原计划增加20%,结果共用了27天完成了这一任务,求原计划每天铺设管道多少米?
如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE=时,求AD的长.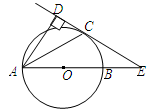
在△ABC和△DEF中,∠C=∠F=90°.有如下五张背面完全相同的纸牌①、②、③、④、⑤,其正面分别写有五个不同的等式,小民将这五张纸牌背面朝上洗匀后先随机摸出一张(不放回),再随机摸出一张.请结合以上条件,解答下列问题.
(1)、你认为和组合,△ABC和△DEF不一定全等,
(2)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌用①、②、③、④、⑤表示);
(3)用两次摸牌的结果和∠C=∠F=90°作为条件,求能满足△ABC和△DEF全等的概率.
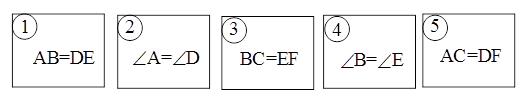
丹东市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了 _________ 名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万名初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
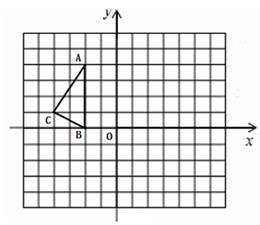
如图,在正方形网格中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC关于原点O对称的△A1B1C1.
(2)平移△ABC,使点A移动到点A2(0,2),画出平移后的△A2B2C2并写出点B2、C2的坐标.
(3)在△ABC、△A1B1C1、△A2B2C2中,△A2B2C2与成中心对称,其对称中心的坐标为.