阅读下列材料并填空。平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
(1)分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
(2)归纳:考察点的个数和可连成直线的条数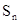 发现:如下表
发现:如下表
| 点的个数 |
可作出直线条数 |
| 2 |
1= |
| 3 |
3=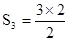 |
| 4 |
6= |
| 5 |
10= |
| …… |
…… |
| n |
 |
(3)推理:平面上有n个点,两点确定一条直线。取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2;即
(4)结论:
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数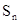 ,发现:(填下表)
,发现:(填下表)
| 点的个数 |
可连成三角形个数 |
| 3 |
|
| 4 |
|
| 5 |
|
| …… |
|
| n |
|
(3)推理: (4)结论:
如图,已知 是 的直径,点 是圆上异于 、 的一点,连结 并延长至点 ,使 ,连结 交 于点 ,连结 .
(1)求证: 是等腰三角形;
(2)连结 并延长,与以 为切点的切线交于点 ,若 , ,求 的长.

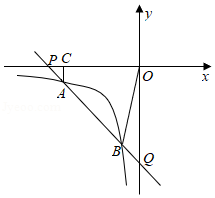
如图,一次函数 的图象与反比例函数 的图象相交于点 , 两点,过点 作 于点 .
(1)求一次函数和反比例函数的表达式;
(2)求四边形 的面积.
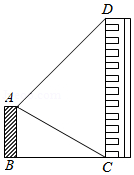
如图, 和 两幢楼地面距离 为 米,楼 高30米,从楼 的顶部点 测得楼 的顶部点 的仰角为 .
(1)求 的大小;
(2)求楼 的高度(结果保留根号).
在疫情期间,为落实“停课不停学”,某校对本校学生某一学科在家学习情况进行抽样调查,了解到学生的学习方式有:电视直播、任课教师在线辅导、教育机构远程教学、自主学习.参与调查的学生只能选择一种学习方式,将调查结果绘制成不完整的扇形统计图和条形统计图.根据如图所示的统计图,解答下列问题.
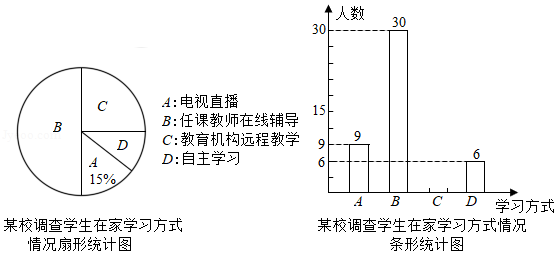
(1)本次接受调查的学生有 名;
(2)补全条形统计图;
(3)根据调查结果,若本校有1800名学生,估计有多少名学生参与任课教师在线辅导?
如图,在 中,点 是边 的中点,连结 并延长到点 ,使 ,连结 .
(1)求证: ;
(2)若 的面积为5,求 的面积.
