(满分12分)如图,在直线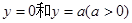 之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校.已知船速为
之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校.已知船速为 ,车速为
,车速为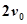 (水流速度忽略不计).若d=2a,求该学生早晨上学时,从家出发到达学校所用的最短时间.
(水流速度忽略不计).若d=2a,求该学生早晨上学时,从家出发到达学校所用的最短时间.
已知椭圆 的右焦点为
的右焦点为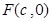 ,上顶点为B,离心率为
,上顶点为B,离心率为 ,圆
,圆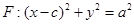 与
与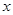 轴交于
轴交于 两点
两点
(Ⅰ)求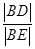 的值;
的值;
(Ⅱ)若 ,过点
,过点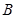 与圆
与圆 相切的直线
相切的直线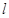 与
与 的另一交点为
的另一交点为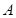 ,求
,求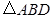 的面积
的面积
如图,四边形 是正方形,
是正方形, ,
,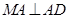 ,
,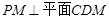 ,
, 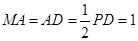
(Ⅰ)求证:平面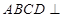 平面
平面 ;
;
(Ⅱ)求三棱锥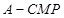 的高
的高 
下表是某单位在2013年1—5月份用水量(单位:百吨)的一组数据:
月份 |
1 |
2 |
3 |
4 |
5 |
用水量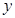 |
4 5 |
4 |
3 |
2 5 |
1 8 |
(Ⅰ)若由线性回归方程得到的预测数据与实际检验数据的误差不超过0 05,视为“预测可靠”,通过公式得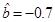 ,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
(Ⅱ)从这5个月中任取2个月的用水量,求所取2个月的用水量之和小于7(单位:百吨)的概率
参考公式:回归直线方程是: ,
,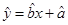
在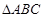 中,角
中,角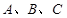 所对的边分别为
所对的边分别为 ,已知
,已知 ,
,
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若 ,求
,求 的取值范围.
的取值范围.
设函数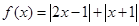 .
.
(Ⅰ)解不等式 ;
;
(Ⅱ)若函数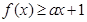 的解集为
的解集为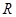 ,求实数
,求实数 的取值范围.
的取值范围.