如图,△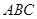 是等边三角形,点
是等边三角形,点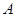 坐标为(-8,0)、点
坐标为(-8,0)、点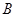 坐标为(8,0),点
坐标为(8,0),点 在
在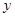 轴的正半轴上.一条动直线从
轴的正半轴上.一条动直线从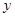 轴出发,以每秒1个单位长度的速度沿
轴出发,以每秒1个单位长度的速度沿 轴向右平移,直线与直线
轴向右平移,直线与直线 交于点
交于点 ,与线段
,与线段 交于点
交于点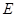 .以
.以 为边向左侧作等边△
为边向左侧作等边△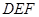 ,
,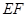 与
与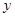 轴的交点为
轴的交点为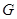 .当点
.当点 与点
与点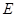 重合时,直线停止运动,设直线的运动时间为(秒).
重合时,直线停止运动,设直线的运动时间为(秒).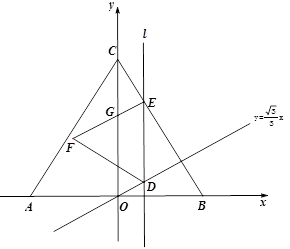
(1)填空:点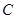 的坐标为 ,四边形
的坐标为 ,四边形 的形状一定是 ;
的形状一定是 ;
(2)试探究:四边形 能不能是菱形?若能,求出相应的的值;若不能,请说明理由.
能不能是菱形?若能,求出相应的的值;若不能,请说明理由.
(3)当t为何值时,点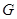 恰好落在以
恰好落在以 为直径的⊙
为直径的⊙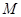 上?并求出此时⊙
上?并求出此时⊙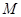 的半径.
的半径.
(如图1),点P将线段AB分成一条较小线段AP和一条较大线段BP,如果 ,那么称点P为线段AB的黄金分割点,设
,那么称点P为线段AB的黄金分割点,设 =k,则k就是黄金比,并且k≈0.618.
=k,则k就是黄金比,并且k≈0.618.
(1)以图1中的AP为底,BP为腰得到等腰△APB(如图2),等腰△APB即为黄金三角形,黄金三角形的定义为:满足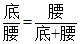 ≈0.618的等腰三角形是黄金三角形;类似地,请你给出黄金矩形的定义: ;
≈0.618的等腰三角形是黄金三角形;类似地,请你给出黄金矩形的定义: ;
(2)如图1,设AB=1,请你说明为什么k约为0.618;
(3)由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分(设S1<S2),如果 ,那么称直线l为该矩形的黄金分割线.(如图3),点P是线段AB的黄金分割点,那么直线CP是△ABC的黄金分割线吗?请说明理由;
,那么称直线l为该矩形的黄金分割线.(如图3),点P是线段AB的黄金分割点,那么直线CP是△ABC的黄金分割线吗?请说明理由;
(4)图3中的△ABC的黄金分割线有几条?
为了加强视力保护意识,小明想在长为4.3米,宽为3.2米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙、丙三位同学设计的方案新颖,构思巧妙.
(1)甲生的方案:如图1,将视力表挂在墙ABEF和墙ADGF的夹角处,被测试人站立在对角线AC上,问:甲生的设计方案是否可行?请说明理由.
(2)乙生的方案:如图2,将视力表挂在墙CDGH上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理课计算得到:测试线应画在距离墙ABEF 米处.
(3)丙生的方案:如图3,根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.图中的△ADF∽△ABC,如果大视力表中“E”的长是多少cm?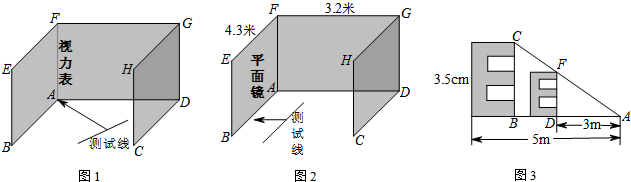
如图,在梯形ABCD中,AD∥BC,AC=AB,AC平分∠DAB,F为BC上一点,且BF=AD,连接DF交AC于E点,连接BE.
(1)求证:BE=DC;
(2)若AD=4,BC=6,求BE的长.
如图,在梯形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAD的平分线AE交BC于E,G是AD的中点,连接DE.
(1)猜想四边形ABED的形状,并说明理由;
(2)当AB与EC满足怎样的数量关系时,EG∥CD?并说明理由.
某班参加校运动会的19名运动员的运动服号码恰是1~19号,这些运动员随意地站成一个圆圈,则一定有顺次相邻的某3名运动员,他们运动服号码数之和不小于32,请你说明理由.