如图所示,直角梯形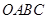 的直角顶点
的直角顶点 是坐标原点,边
是坐标原点,边 、
、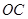 分别在
分别在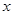 轴、
轴、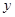 轴的正半轴上,
轴的正半轴上,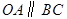 ,
,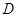 是
是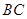 上一点,
上一点,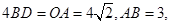
 ,其中点
,其中点 、
、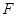 分别是线段
分别是线段 、
、 上的两个动点,且始终保持
上的两个动点,且始终保持 。
。直接写出点
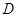 的坐标
的坐标求证:
 ;
;当
 是等腰三角形时,△AEF关于直线EF的对称图形为
是等腰三角形时,△AEF关于直线EF的对称图形为 ,求
,求 与五边形OEFBC的重叠部分的面积.
与五边形OEFBC的重叠部分的面积.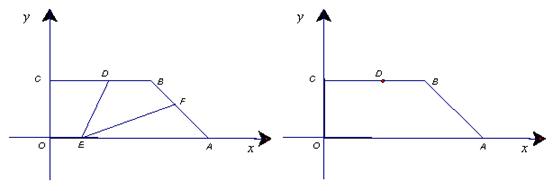
备用图
如图所示, 是 的直径, 和 分别切 于 , 两点, 与 有公共点 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

列方程(组 解应用题
某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为 的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长 ,另外三面用 长的篱笆围成,其中一边开有一扇 宽的门(不包括篱笆).求这个茶园的长和宽.

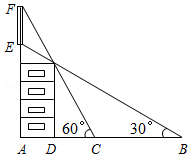
如图所示,某建筑物楼顶有信号塔 ,卓玛同学为了探究信号塔 的高度,从建筑物一层 点沿直线 出发,到达 点时刚好能看到信号塔的最高点 ,测得仰角 , 长7米.接着卓玛再从 点出发,继续沿 方向走了8米后到达 点,此时刚好能看到信号塔的最低点 ,测得仰角 .(不计卓玛同学的身高)求信号塔 的高度(结果保留根号).
某校组织开展运动会,小明和扎西两名同学准备从100米短跑(记为项目 ,800米中长跑(记为项目 ,跳远(记为项目 ,跳高(记为项目 ,即从 , , , 四个项目中,分别选择一个项目参加比赛.请用画树状图或列表法求两名同学选到相同项目的概率.
如图, 中, 为 边上的一点, ,以线段 为边作 ,使得 , .求证: .
