(12分)用简单随机抽样从含有8个个体的总体中抽取一个容量为2的样本．问：
①总体中的某一个体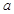
在第一次抽取时被抽到的概率是多少?
②个体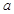在第1次未被抽到，而第2次被抽到的概率是多少?
③在整个抽样过程中，个体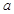被抽到的概率是多少?
(1)证明：l经过定点；
(2)若直线l交x轴负半轴于A，交y轴正半轴于B，△AOB的面积为S，求S的最小值并求此时直线l的方程；
(3)若直线不经过第三象限，求k的取值范围．
已知向量a＝(sin θ，－2)与b＝(1，cos θ)互相垂直，其中θ∈
(1)求sin θ和cos θ的值；
(2)若5cos(θ－φ)＝3cos φ，0＜φ＜，求cos φ的值．
在△ABC，已知2·＝||·
||＝3BC2，求角A、B、C的大小
已知a＝，b＝，其中0<α<β<π.
(1)求证：a＋b与a－b互相垂直；
(2)若ka＋b与ka－b(k≠0)的长度相等，求β－α.
已知向量a＝，b＝，且x∈，
(1)求a·b及|a＋b|；
(2)若f(x)＝a·b－2λ|a＋b|的最小值是－，求λ的值