如图,在侧棱垂直底面的四棱柱 中, , 是 的中点, 是平面 与直线 的交点.
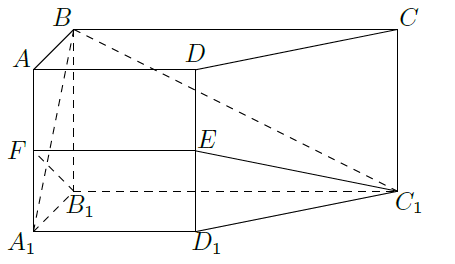
(1)证明:
(i)
;
(ii)
平面
;
(2)求
与平面
所成的角的正弦值.
(本小题满分12分)
右图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人
(I)求该专业毕业总人数N和90~95分数段内的人数 ;
;
(II)现欲将90~95分数段内的 名人分配到几所学校,从中安排2人到甲学校去,若
名人分配到几所学校,从中安排2人到甲学校去,若 人中仅有两名男生,求安排结果至少有一名男生的概率.
人中仅有两名男生,求安排结果至少有一名男生的概率.
(本小题满分12分)
已知直线两直线 中,内角A,B,C对边分别为
中,内角A,B,C对边分别为 时,两直线恰好相互垂直;
时,两直线恰好相互垂直;
(I)求A值;
(II)求b和 的面积
的面积
(本小题满分14分)
已知抛物线 上一点
上一点 到其焦点F的距离为4;椭圆
到其焦点F的距离为4;椭圆 的离心率
的离心率 ,且过抛物线的焦点F.
,且过抛物线的焦点F.
(I)求抛物线 和椭圆
和椭圆 的标准方程;
的标准方程;
(II)过点F的直线 交抛物线
交抛物线 于A、B两不同点,交
于A、B两不同点,交 轴于点N,已知
轴于点N,已知 ,求证:
,求证: 为定值.
为定值.
(III)直线 交椭圆
交椭圆 于P,Q两不同点,P,Q在x轴的射影分别为
于P,Q两不同点,P,Q在x轴的射影分别为 ,
, ,
, ,若点S满足:
,若点S满足: ,证明:点S在椭圆
,证明:点S在椭圆 上.
上.
(本小题满分13分)
已知 处的切线为
处的切线为
(I)求 的值;
的值;
(II)若 的极值;
的极值;
(III)设 ,是否存在实数
,是否存在实数 (
( ,为自然常数)时,函数
,为自然常数)时,函数 的最小值为3.
的最小值为3.
(本小题满分12分)
已知 是等差数列
是等差数列 的前n项和,数列
的前n项和,数列 是等比数列,
是等比数列, 恰为
恰为 的等比中项,圆
的等比中项,圆 ,直线
,直线 ,对任意
,对任意 ,直线
,直线 都与圆C相切.
都与圆C相切.
(I)求数列 的通项公式;
的通项公式;
(II)若 时,
时, 的前n项和为
的前n项和为 ,求证:对任意
,求证:对任意 ,都有
,都有