（本小题满分10分）
某电子科技公司遇到一个技术性难题，决定成立甲、乙两个攻关小组，按要求各自独立进行为期一个月的技术攻关，同时决定对攻关限期内攻克技术难题的小组给予奖励. 已知此技术难题在攻关期限内被甲小组攻克的概率为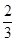
，被乙小组攻克的概率为
，
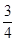（1）设
为攻关期满时获奖的攻关小组数，求的分布列及数学期望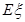
；
（2）设
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方，记“函数
在定义域内单调递增”为事件C，求事件C发生的概率；
（本小题满分12分）
设抛物线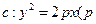
＞0）上有两动点A、B（AB不垂直
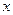轴），F为焦点，且
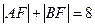，又线段AB的垂直平分线经过定点Q（6，0），求抛物线方程。
（本小题满分12分）
|
棱长为1的正方体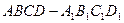
中，P为DD1中点，O1、O2、O3分别为面
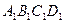、面
、面
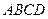的中心。
。
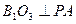（本小题满分12分）
已知椭圆的两顶点与双曲线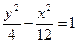
的焦点重合，它们的离心率之和为
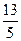，若椭圆的焦点在
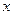轴上，求椭圆的方程。
（本小题满分12分）
已知
方程
有两个不相等的负实根，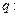
方程
无实数根，若“
或
”为真，“且”为假，求实数
的取值范围。
在直角坐标系
中，直线
与抛物线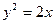
相交于A、B两点。
（1）求证：“如果直线过点T（3，0），那么
=3”是真命题；
（2）写出（1）中命题的逆命题，判断它是真命题还是假命题，并说明理由
